
EL TEOREMA DE BELL

Ya desde su primera formulación en los años 30, la mecánica cuántica recibió objeciones; algunas más superficiales y otras más serias que, si bien no la invalidan ni mucho menos, sí que señalan puntos que el formalismo, o su interpretación, debería aclarar; progresando sin duda en sus éxitos experimentales, pero con un ojo puesto en aquellas cuestiones fundamentales que no sean puramente lingüísticas. La historia que nos atañe aquí es compleja, y es fácil confundir lo sutil con lo trivial, pero vamos a echar un vistazo a los argumentos centrales.
La más célebre de las mencionadas objeciones a la interpretación ortodoxa de la mecánica cuántica se halla en el famoso artículo de Einstein, Podolski y Rosen, abreviadamente EPR. En el mismo, se propone un concepto de realidad de una magnitud física que parece intachable, los llamados elementos de realidad:
"Si, sin perturbar en modo alguno un sistema, podemos predecir con certeza (esto es, con probabilidad igual a uno) el valor de una cantidad física, entonces existe un elemento de realidad física correspondiente a esta cantidad física."
EPR plantean: ¿Podemos preparar un sistema físico en un estado en el que observables a los que la mecánica cuántica (MC en lo que sigue) asigna un carácter de incompatibles arrojen un valor cierto? EPR proponen tenderle esta "trampa" a la MC preparando un sistema compuesto por dos subsistemas que viajan a zonas causalmente separadas en las que se ejecutan las mediciones correspondientes simúltaneamente en el referencial del laboratorio. EPR plantean el problema como una disyuntiva: o bien la MC es incompleta (existen elementos de realidad no cubiertos por la descripción cuántica), o las cantidades correspondientes a operadores que no conmutan no pueden tener valores definidos simultáneamente, y a continuación argumentan haber encontrado un ejemplo de tales cantidades. El argumento original de EPR es algo ingenuo, utilizando ondas planas para su razonamiento, y centrando su discusión en las variables de posición y momento lineal, en clara omisión de lo que hoy sabemos: que no es posible preparar un estado completamente definido en ambas variables posición y momento lineal, con lo cual nunca tendremos correlaciones exactas, ni siquiera en principio, para ambos subsistemas, ya que las relaciones de indeterminación son constricciones sobre las dispersiones de las variables no sobre los errores sistemáticos de los aparatos de medición. En otras palabras: cualquier estado conjunto que preparemos de dos partículas vendrá afectado de indeterminaciones en coordenadas y momentos lineales de su centro de masa. En cualquier descripción realista de esta preparación habrá unos ciertos ΔXCM, ΔPCM que harán que incluso la determinación ideal de la posición de una de las partículas no permita garantizar que la segunda partícula tiene posición asignable con certeza, pues la suma X(1)CM+X(2)CM no es nula de manera exacta (con dispersión nula). Otro tanto se puede decir para el momento lineal.
Esta objeción se supera con el espín, para el cual sí es posible preparar estados con dispersión total nula para una variable aditiva respecto a los subsistemas, lo que nos habilita para definir anticorrelaciones exactas dentro del formalismo de la MC.
Se atribuye a David Bohm ( Max Jammer, 1974) trasladar la discusión al momento angular de espín. Un sistema de espines preparado en el estado singlete viene dado por:
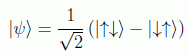
Este estado es famoso en la física por diversos motivos, apareciendo en teoría de grupos, y en particular en la formulación del isospín. Esta no es en absoluto una configuración exótica: cualquier sistema de dos espines 1/2 enfriado suficientemente, emite radiación hasta caer a un singlete. Baste decir que, aunque para su escritura hemos sugerido una configuración particular en términos de una dirección nominal (superposición de la función de onda con espines antiparalelos menos la intercambiada), en realidad es simétrico bajo rotaciones. Es decir:
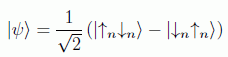
para cualquier vector unitario de referencia n.
El singlete de espín, al contrario que los estados de posición y momento lineal (incluso en el caso más favorable de paquetes mínimos, o de indeterminación mínima), sí tiene las características deseadas de presentar correlaciones exactas (que en este contexto se llaman anticorrelaciones, por motivos que veremos), al menos en principio (si descartamos el efecto de ruido de los detectores, que siempre está presente). Efectivamente, si J representa el momento angular total, según el principio de indeterminación, en su versión más general, para, p. ej. Jx y Jy:
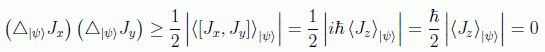
ya que el estado singlete de dos partículas con dos estados de
espín ("arriba" y "abajo") el singlete satisface
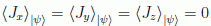 .
Como
.
Como 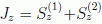 (donde
los superíndices (1) y (2) entre paréntesis denotarán a
partir de ahora "partícula 1" y "partícula 2"), se
deduce que la medición de la componente de espín según
una dirección establecida para una partícula permite
asegurar que la componente de espín según la misma
dirección para la segunda partícula es igual y opuesta: El
sistema presenta indeterminación en sus partes (Sz=+1 o
Sz=-1 con iguales probabilidades de 0.5), y sin embargo
certeza en el total (Jz=0 con probabilidad 1); con lo cual,
si en una de las partículas el espín Sz, p. ej.,
resulta positivo, en la otra ha de ser negativo y de igual magnitud.
De ahí el nombre de "anticorrelaciones". Se puede ver más
en detalle, calculando los valores esperados cuánticos:
(donde
los superíndices (1) y (2) entre paréntesis denotarán a
partir de ahora "partícula 1" y "partícula 2"), se
deduce que la medición de la componente de espín según
una dirección establecida para una partícula permite
asegurar que la componente de espín según la misma
dirección para la segunda partícula es igual y opuesta: El
sistema presenta indeterminación en sus partes (Sz=+1 o
Sz=-1 con iguales probabilidades de 0.5), y sin embargo
certeza en el total (Jz=0 con probabilidad 1); con lo cual,
si en una de las partículas el espín Sz, p. ej.,
resulta positivo, en la otra ha de ser negativo y de igual magnitud.
De ahí el nombre de "anticorrelaciones". Se puede ver más
en detalle, calculando los valores esperados cuánticos:
El valor esperado cuántico del cuadrado de
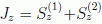 es:
es:
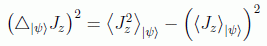
Pero:
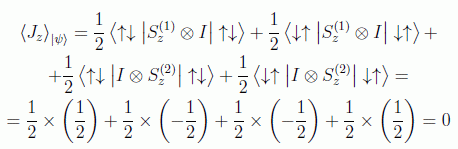
Obsérvese para lo previo que:
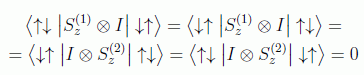
con lo cual:
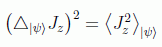
Desarrollando el cuadrado del momento angular total:
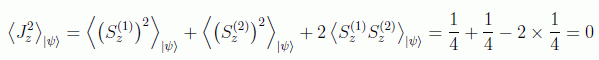
Estos son los cálculos:
Sustituyendo 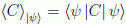 con
con 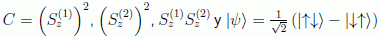 , y teniendo en
cuenta que, en el espacio producto, lo que estamos promediando en
realidad son los operadores producto:
, y teniendo en
cuenta que, en el espacio producto, lo que estamos promediando en
realidad son los operadores producto: 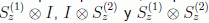 , y que
además
, y que
además 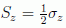 (si las partículas son
de espín 1/2, que es lo que supondremos en adelante):
(si las partículas son
de espín 1/2, que es lo que supondremos en adelante):
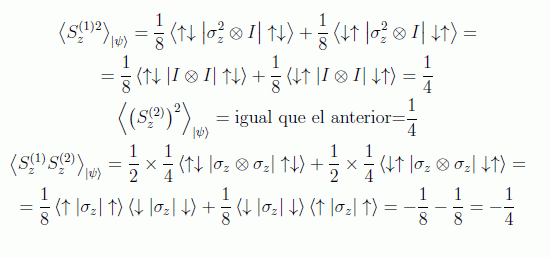
Observación: Ninguno de los términos cruzados <↓↑|C|↑↓> (con C cualquiera de los operadores función de σz) contribuye.
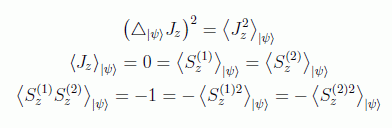
Con lo que:
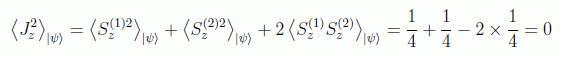
Un esquema que quizá pueda ayudar para el desarrollo de todos estos cálculos, incluyendo los que veremos más adelante para el teorema de Bell, es:

Lo que quisiera cualquiera al que le convenza el argumento EPR, y cuya toma de posición sea que la MC es una teoría incompleta, es encontrar unas ciertas variables, que genéricamente llamaremos {λ}, y que modelen la descripción matemática de aquella supuesta parte de la realidad física que la MC no describe. Estas {λ} no son meras suposiciones metafísicas, sino que tienen dos trabajos que hacer: (1) Valores definidos de las mismas deberían conducir a valores definidos de los elementos de realidad; y (2) Valores promediados de las mismas para cierta distribución de probabilidad ρ({λ}) deberían conducir a dispersiones en las variables (en general, no compatibles) que tenga sentido medir y que sean consistentes con las proporcionadas por la MC. En otras palabras: son las supuestas variables cuya estadística debe dar la MC de modo análogo a como la mecánica estadística de las posiciones y velocidades atómicas da lugar a la termodinámica.
¿Por qué se nos exige una toma de posición? Recuérdese que EPR plantea una disyuntiva: O bien la MC es incompleta,o existen variables físicas que no pueden tener valores definidos simultáneamente. Téngase presente que, para quien está completamente convencido de que la MC es correcta y completa, no hay problema: ¡Por supuesto que hay variables físicas que no pueden tener valores definidos simultáneamente! Precisamente las que no conmutan.
Cuando un sistema cuántico compuesto por dos subsistemas (con grados de libertad independientes) se halla en un estado conjunto tal que:
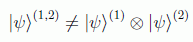
decimos que el sistema 1 está enredado con el sistema 2. Basta para ello que se cumpla, por ejemplo:
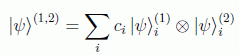
aunque el estado enredado más general es (de hecho, el estado cuántico más general de un sistema compuesto):
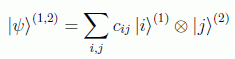
En el estudio de la
decoherencia,
el enredamiento, la
medición
o la
teoría
cuántica de la información, este concepto de enredamiento
se desarrolla en forma más concreta. Véase que los estados
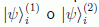 referidos
podrían no ser ortogonales.
Cuando ambos conjuntos son ortogonales:
referidos
podrían no ser ortogonales.
Cuando ambos conjuntos son ortogonales:
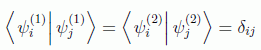
entonces el índice i se presta a la asignación de un
observable,
que por construcción sería de la forma
(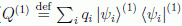 ).
Asimismo, se presta a la asignación de un observable del sistema
2 que puede usarse para medir Q(1) en el
subsistema 1. En otras palabras, un sistema compuesto que presenta
enredamiento en esta forma, es un sistema en el que la no
factorizabilidad se produce de tal forma que los coeficientes de
enredamiento cij en el estado general forman una
matriz diagonal. Es una observación de
Wojciech
Zurek que muchos sistemas físicos tienden a adoptar esta forma
cuando se centra la discusión en una parte (1) que tiene pocos
grados de libertad y una parte (2) que es típicamente
"ambiental" (con muchos grados de libertad) y se tiene en cuenta
que las interacciones son locales (funciones puntuales de la
posición). Este concepto de Zurek se llama
einselection,
o "superselección de observables inducida por el ambiente".
Dicho de otra forma: el ambiente tiende a favorecer interacciones
recurrentes a través de cualquier índice discreto i en el
que centremos nuestra atención, rompiendo así la
coherencia
cuántica. Es una cuestión que tiene que ver con lo peculiar
de describir lo que le ocurre a un átomo que está enredado
con ~1023 átomos.
).
Asimismo, se presta a la asignación de un observable del sistema
2 que puede usarse para medir Q(1) en el
subsistema 1. En otras palabras, un sistema compuesto que presenta
enredamiento en esta forma, es un sistema en el que la no
factorizabilidad se produce de tal forma que los coeficientes de
enredamiento cij en el estado general forman una
matriz diagonal. Es una observación de
Wojciech
Zurek que muchos sistemas físicos tienden a adoptar esta forma
cuando se centra la discusión en una parte (1) que tiene pocos
grados de libertad y una parte (2) que es típicamente
"ambiental" (con muchos grados de libertad) y se tiene en cuenta
que las interacciones son locales (funciones puntuales de la
posición). Este concepto de Zurek se llama
einselection,
o "superselección de observables inducida por el ambiente".
Dicho de otra forma: el ambiente tiende a favorecer interacciones
recurrentes a través de cualquier índice discreto i en el
que centremos nuestra atención, rompiendo así la
coherencia
cuántica. Es una cuestión que tiene que ver con lo peculiar
de describir lo que le ocurre a un átomo que está enredado
con ~1023 átomos.
Subsistemas enredados de esta forma peculiar, que es "diagonal" en cierto índice que podría formar parte o no de un conjunto completo de observables compatibles de cualquiera de ambos, se puede definir una entropía que caracteriza el nivel de enredamiento de ambos. Si ρ es la matriz densidad del sistema conjunto:
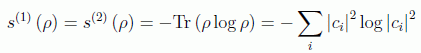
donde "Tr" representa la traza de un operador lineal. Es decir:
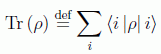
para cierta base del espacio de Hilbert 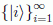 .
.
Funciones como log ρ, que admiten un desarrollo en serie, se definen para operadores diagonalizables de la manera siguiente si admiten un desarrollo en serie de Taylor:
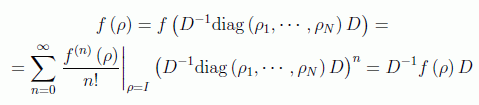
ya que:
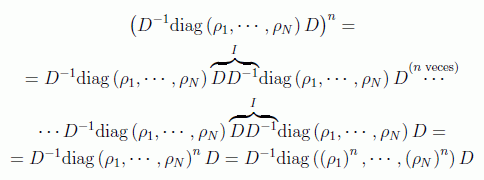
donde D es la matriz que diagonaliza ρ:
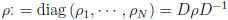 .
.
La definición de entropía no es más que la usual en MC, pero referida a los coeficientes (probabilidades pi=|ci|2) del desarrollo conjunto de los subsistemas, y recibe el nombre de entropía de enredamiento. Cuando dos sistemas están enredados en la forma anterior respecto a estados ortogonales , su entropía de enredamiento es una propiedad común, y se puede obtener para el subsistema 1 promediando sobre los estados del subsistema 2, o viceversa:
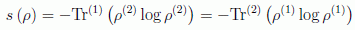
Es decir, primero promediamos sobre todos los estados del subsistema 2 para obtener la matriz densidad de 1, y después tomamos trazas usando la descomposición espectral de la identidad de 1; o viceversa.
"Por localidad quiero decir algo como los axiomas de Atiyah-Segal para cobordismos Riemannianos"
(Tomado de un foro de física teórica en Internet)
3.325. Con el fin de evitar tales errores debemos hacer uso de un lenguage de signos que los excluya evitando usar el mismo signo para símbolos diferentes y evitando usar en una forma superficial similar signos que tienen modos diferentes de significación: es decir, un lenguage de signos que esté gobernado por una gramática lógica, por sintaxis lógica [...]
Ludwig Wittgenstein: Tractatus Logico-Philosophicus, Sección 3.325
El término "localidad" en física está afectado del síndrome de la torre de Babel: aparece en la literatura con significados que van desde sutilmente distintos a completamente distintos, lo cual crea mucha confusión. Intentaremos aclarar las diferencias.
L1. Localidad en teoría de la matriz de scattering: La transformada de Fourier de una amplitud de scattering con soporte compacto es exponencialmente acotada y analítica en el momento lineal. Es un concepto técnico que no nos interesa aquí y que Arkani-Hamed explica en este vídeo en inglés (hacia 6:20).
L2. Localidad algebraica, analítica o si se
quiere,matemática (esta acepción es puramente
conversacional, pero es muy usual): A es función local de B
si un punto en el espacio de las A (valor numérico a, de
A) determina un punto en el espacio de las B (valor numérico
b, de B). El significado de esto es "desarrollo en variables
que conmutan todas dos a dos". Los matemáticos hablan de un
"desarrollo no local" cuando manejan expresiones polinómicas
en variables que no conmutan; ej.:
(A+B)2=A2+AB+BA+B2; con AB≠BA, o más
simplemente, cuando A=f(B); con AB≠BA. ¿Por
qué llaman a esto los matemáticos "no local"? Porque si
AB≠ BA, (suponiendo, por simplificar, que tanto A como B
son
autoadjuntos)
todos los valores puntuales (numéricos) de B están
en cualquier valor puntual (numérico) de A:
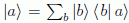 , que no es más que una manera
elegante,
inventada
por Dirac, de escribir la transformación de Fourier.
, que no es más que una manera
elegante,
inventada
por Dirac, de escribir la transformación de Fourier.
Esta forma de no localidad nos interesa, porque, como veremos, las variables del experimento EPR para el espín son no locales en este sentido cuando uno acepta que la proposición |a><a| (¡los proyectores son proposiciones!) para una partícula implica su negación (I-|a><a|) para la otra partícula. La consecuencia es que la diagramática de Venn no es válida para proposiciones referidas a proyecciones de espín. Esta es la clave de la brillante idea de EPR: sortear la incompatibilidad cuántica, que es aplicable únicamente a operadores que actúan en el espacio de estados de una partícula y que no conmutan (p. ej. [S1,S2]≠0) trasladándola a proposiciones sobre operadores que sí conmutan ([Sx(1),Sy(2)]=[Sx(1)⊗ I,I ⊗ Sy(2)]=0), pero relativos a la otra partícula, utilizando los principios de conservación.
L3. Localidad en teoría de campos: Las interacciones son funciones locales en el sentido de que los acoplamientos entre variables de campo en la lagrangiana se expresan en el mismo punto: Ψi(x)Ψj(x), y nunca en puntos diferentes: Ψi(x)Ψj(x+a). Una caracterización equivalente es que la lagrangiana no depende de derivadas espaciales de orden arbitrariamente alto. Concepto técnico también que no es el relevante aquí.
L4. Causalidad del problema de Cauchy o, si se quiere, localidad einsteniana: A veces se habla de "localidad" cuando a lo que se hace referencia realmente es a esto. Un problema de evolución es causal cuando los datos de Cauchy (condiciones iniciales) se propagan dentro de conos causales. Este concepto se solapa con el de causalidad en teoría cuántica de campos relativista. Estas formulaciones de la causalidad en términos del propagador también tienen un sentido técnico que no nos interesa aquí.
L5. No localidad en sentido de Bell, Clauser, Shimony, etc., es decir, no separabilidad en el sentido de efectos a distancia entre sistemas enredados (entangled). (Mejor aquí hablar de no localidad, ya que la peculiar descripción de los sistemas físicos que hace la MC es no local en este sentido preciso.) Esta no localidad específica de la MC se da por la concurrencia de dos aspectos diferentes:
(1) Los sistemas cuánticos están representados por campos (funciones de la posición y el tiempo), que satisfacen el principio de superposición.
(2) El espacio de estados de un sistema cuántico de varias partículas es un producto externo de los espacios de estados individuales.
Los campos clásicos, que cumplen el principio de superposición, no presentan enredamiento. P. ej., tanto el campo gravitatorio como el campo electromagnético clásicos, son magnitudes físicas que se obtienen por superposición de los efectos inducidos por todas las fuentes (cargas y corrientes) ambientales para contribuir a un único valor, g(x,t), E(x,t) , B(x,t), etc. Los campos clásicos, por tanto, cumplen (1), pero no cumplen (2).
Las partículas clásicas no presentan enredamiento. Es cierto que en la formulación estadística de Liouville de la mecánica clásica, los sistemas con interacción se enredan en su densidad de probabilidad en el espacio de fases: ρ(x1,···,xn;p1,···,pn)≠ρ1(x1,p1)···ρn(xn,pn), pero lo hacen sobre colectividades ideales llamadas colectividades de Gibbs. Los únicos observables de esta teoría son cosas como la presión, la temperatura, etc., que se definen como promedios sobre colectividades.
Por el contrario, los sistemas cuánticos de varias partículas, se superponen, se propagan y además, sus estados dinámicos se construyen por productos de estados individuales. Esta es la combinación peculiar que constituye la no separabilidad cuántica, como algunos han propuesto llamarla para distinguirla de otros tipos de hipotéticas acciones a distancia. La consecuencia de esto es que será posible copiar situaciones físicas (estados) instantáneamente y a distancia, pero no transmitir datos o resultados de la misma manera.
Recuérdese que dijimos que las supuestas variables ocultas {λ} tenían dos trabajos que hacer:
(1) Valores definidos de {λ} deben conducir a valores definidos de los elementos de realidad.
(2) Valores promediados de {λ} para cierta distribución de probabilidad ρ({λ}) deben conducir a dispersiones en las variables consistentes con las proporcionadas por la MC.
El teorema de Bell demuestra que (2) no es posible para cualquier observable que tenga sentido medir. Los teoremas de Gleason, de Kochen-Specker así como el análisis de Greenberger-Horne-Zeilinger-Mermin (GHZM), algunos de los cuales discutiremos brevemente, se dirigen a demostrar la imposibilidad de (1). Son la continuación de un teorema de John Von Neumann que se dirige a demostrar la imposibilidad de la mera existencia de elementos de realidad.
El teorema de Bell tiene un lema previo muy sencillo (en matemáticas es tradicional llamar "lema" a un resultado breve que va a usarse después para una demostración más elaborada). El lema consiste en un resultado que permite traducir proposiciones sobre la partícula 1 en proposiciones sobre la partícula 2. En concreto, y como ya hemos apuntado, cuando se mide la componente de espín de una de las partículas respecto a cierta dirección de referencia y el resultado es +1, la componente de espín de la otra partícula respecto a la misma dirección de referencia es -1, y viceversa. Llamaremos a este lema CHSHB-1(1).:
CHSHB-1: Siempre que σ(1)·n=+1, σ(2)·n=-1.
Observaciones:
(1) Este resultado no es propiamente cuántico ni clásico; es la consecuencia de un principio de conservación que se cumple de manera exacta tanto en la mecánica clásica como en la cuántica. La anticorrelación que se pone de manifiesto es la deducida de la conservación del momento angular: si el sistema no ha adquirido momento angular orbital debido a la desintegración, sus espines deben estar perfectamente compensados.
(2) σ·n es un observable de espín según una dirección arbitraria. Denotando en lo que sigue por los índices 1, 2 y 3 los ejes espaciales x, y y z respectivamente, si n=(n1,n2,n3) es el vector unitario en la dirección espacial dada, el vector σ=(σ1,σ2,σ3) es un símbolo con tres componentes que son las matrices de Pauli:
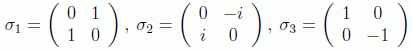
Propiedades inmediatas de las matrices de Pauli son:
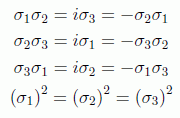
Lo que se puede expresar abreviadamente como:
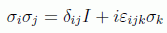
El segundo resultado, que es el teorema en sí mismo, \emph{no tiene nada que ver con el espín.} Es una consecuencia simple del álgebra conmutativa de tres variables booleanas. Afirma que para tres proposiciones cualesquiera relativas a tres variables estadísticas que forman parte de un álgebra booleana, siempre se satisface la siguiente desigualdad(2):
CHSHB-2: 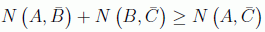
En palabras: el número de veces que se cumple A y no B más el número de veces que se cumple B y no C es mayor o igual que el número de veces que se cumple A y no C. Lo profundo de este teorema es que ¡el espín viola esta desigualdad en ciertos casos!.
Demostrar CHSHB-2 es fácil. Obsérvese en las figuras: que:
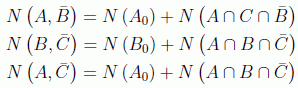
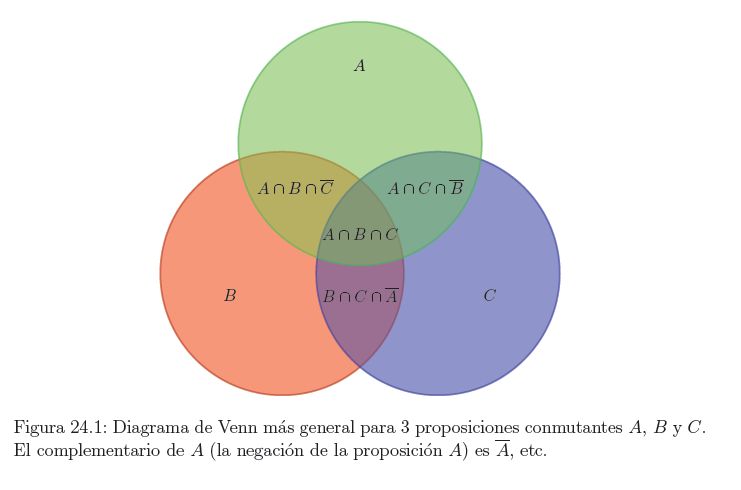
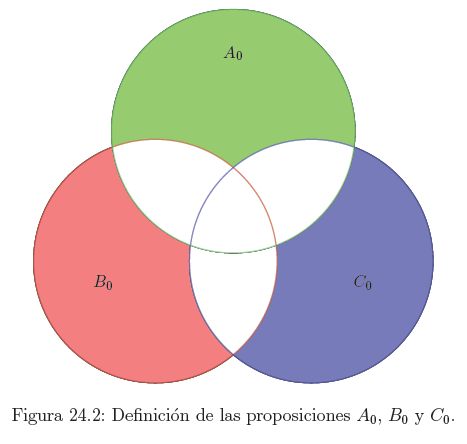
Donde hemos llamado A0 a la parte de A que no está ni en B ni en C, y análogamente para B0 y C0, como se puede ver en la figura 24.2.
En la imagen puede verse claramente que:
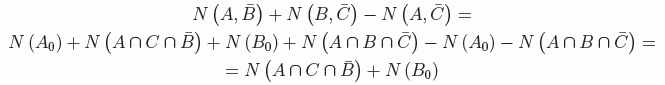
Pero 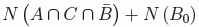 es
obviamente mayor o igual que cero. Con lo que hemos demostrado que:
es
obviamente mayor o igual que cero. Con lo que hemos demostrado que:
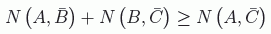
Pues bien, esto es lo que Bell demostró: Existen elecciones particularmente maliciosas de proposiciones A, B y C para las que la mecánica cuántica predice lo opuesto:
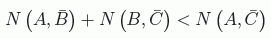
Esta es una conocida perversa elección:

Para demostrarlo hay que tener en cuenta que el número de casos
favorables es proporcional a la probabilidad
(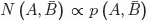 , etc.), y
que esta a su vez se obtiene mediante los cuadrados hermíticos
de las amplitudes. Además, hay que tener en cuenta que la
negación de la proposición A para una partícula equivale
a la afirmación de la misma proposición para la otra
partícula (véase OBS3 más adelante):
, etc.), y
que esta a su vez se obtiene mediante los cuadrados hermíticos
de las amplitudes. Además, hay que tener en cuenta que la
negación de la proposición A para una partícula equivale
a la afirmación de la misma proposición para la otra
partícula (véase OBS3 más adelante):
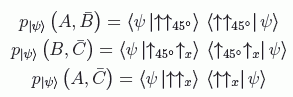
Como muchas veces en física, existe una o varias maneras difíciles de demostrarlo y una única manera sencilla. La escritura sugerida en las ecuaciones anteriores es la difícil. La manera más sencilla utiliza las siguientes observaciones:
OBS1:
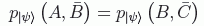
ya que la configuración 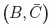 es idéntica
a la configuración
es idéntica
a la configuración 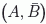 , pero rotada
45º en sentido positivo respecto al eje y.
, pero rotada
45º en sentido positivo respecto al eje y.
OBS2:
El proyector sobre la dirección de espín
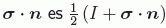 .
.
Comprobación: Para 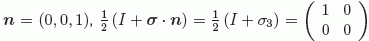 . Como la dirección del eje z es en realidad arbitraria, la expresión
es invariante. Pero comprobemos además que
. Como la dirección del eje z es en realidad arbitraria, la expresión
es invariante. Pero comprobemos además que
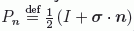 es en efecto un proyector:
es en efecto un proyector:
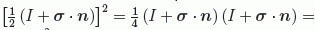
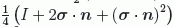 .
Pero como de las propiedades de las matrices de Pauli se deduce:
.
Pero como de las propiedades de las matrices de Pauli se deduce:
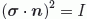 , se
deduce inmediatamente que
, se
deduce inmediatamente que
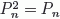 .
.
OBS3:
La negación de A para la partícula 1 equivale a la afirmación de A para la 2 (análogamente para B y C).
Necesitaremos también la forma del operador de espín "a 45º'', refiriéndonos a la dirección que está a 45º entre el eje x y el eje z:
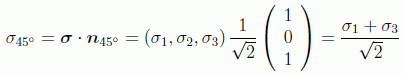
Todo esto permite escribir:
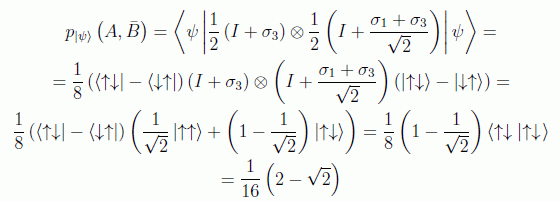
Recordando la ecuación de la observacion 1 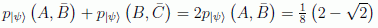
Por otra parte:
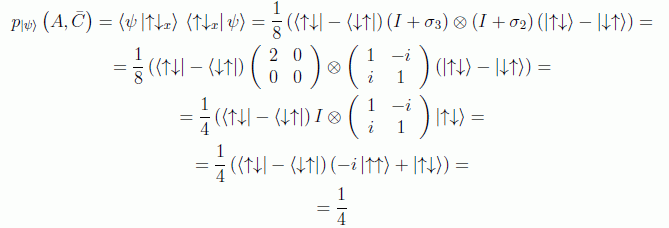
Pero definiendo:
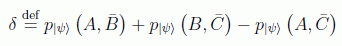
tenemos:
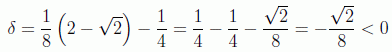
En contradicción con la desigualdad de Bell.
Si Pr es un proyector que proyecta sobre un cierto |r> (podemos pensar en Pr como |r><r| o como una cierta expansión Σα|r,α> < r,α|) y ρ es un estado mezcla arbitrario (podemos pensar en ρ como |ψ>< ψ| o una mezcla estadística de varios |ψi> < ψi|, es decir Σipi|ψi> < ψi|, con 0≤ pi≤1, Σipi=1), la única función posible que define la probabilidad de obtener el resultado r es esencialmente:
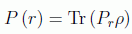
Como la función Tr(Prρ) es continua sobre la esfera unidad como función de ρ, es imposible que adopte los valores 0 y 1 sobre la misma. Con la esfera unidad aquí nos referimos a una esfera de estados de espín, es decir, a todos los |ψ> tales que ρ=|ψ>< ψ| en la ecuación anterior, y donde σ·n|ψ> =±|ψ>, y n es una dirección arbitraria sobre la 2-esfera espacial de radio 1. Una función continua sobre este conjunto no puede tomar los valores 0 y 1 sin tomar todos los valores intermedios posibles.
La consecuencia de esto es que es imposible resolver todas las proposiciones de espín posibles con unas variables deterministas adicionales que fijen sus valores. Podríamos decir que este es un teorema de tipo ontológico: los valores definidos del espín no pueden ser la \href{http://es.wikipedia.org/wiki/Conjunto_imagen}{imagen matemática} de un cierto conjunto matemático en una correspondencia punto a punto.
El teorema de Kochen-Specker es la elaboración de una cuestión planteada primero por Von Neumann y analizada más tarde por Bell. La idea de la que parte esta línea de investigación es un teorema de Von Neumann. El argumento de Von Neumann establece que, dado que si A y B son observables
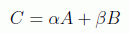
también es un observable; y dado que los promedios mecanocuánticos deben satisfacer:
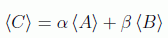
si queremos que A, B, C estén definidos (definitud de valores o value definiteness en la literatura), debería cumplirse:
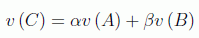
para una cierta función v que asigna un valor definido a cada
uno de estos observables. Von Neumann afirma que esta
construcción es imposible en general para conjuntos de
observables de espín en la MC. Bell dio el ejemplo
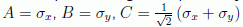 como una
excepción posible, ya que
como una
excepción posible, ya que
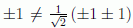 para ninguna
elección de estas variables. Pero al mismo tiempo Bell
también observó que la premisa anterior
propuesta por Von Neumann era muy severa. Debería exigirse que
esto fuera cierto, no en general, sino únicamente para
observables compatibles.
para ninguna
elección de estas variables. Pero al mismo tiempo Bell
también observó que la premisa anterior
propuesta por Von Neumann era muy severa. Debería exigirse que
esto fuera cierto, no en general, sino únicamente para
observables compatibles.
Pues bien, el teorema de Kochen-Specker afirma que ni siquiera esta asignación es posible si a la vez admitimos la validez de la MC y para ciertas elecciones finitas y compatibles de proposiciones de espín. La única escapatoria es que la función v, en lugar de ser una asignación universal, sea una asignación dependiente de aspectos adicionales (el contexto). Es decir, que la definitud sea contextual, en lugar de una propiedad intrínseca de los sistemas físicos.
Así como el teorema de Bell se interpreta como la demostración de que no es posible la coexistencia del realismo local con la MC, el teorema de Kochen-Specker se interpreta como la demostración de que no es posible la coexistencia del realismo no contextual o intríseco, si se quiere, con la MC. En otras palabras: Hay ciertos observables en el espacio interno del espín que, aun siendo compatibles, no pueden tener definitud simultánea; no pueden por tanto considerarse propiedades intrínsecas del sistema.
Este argumento se añadió a la cuestión de las variables ocultas en 1990 por Daniel M. Greenberger, Michael A. Horne y Anton Zeilinger , posteriormente simplificado por los mismos autores más Abner Shimony tras una sugerencia de David Mermin, todo en el mismo año. Aquí presentamos la idea en una forma que sigue estrechamente la exposición que dio Sidney Coleman en su famosa conferencia Quantum Mechanics in Your Face. Es la exposición más sencilla que yo conozco. Como dice el mismo Coleman: "Si alguien te despertara a altas horas de la madrugada y pusiera una pistola contra tu cabeza, podrías reproducir el argumento inmediatamente".
Se trata de un sistema compuesto por tres partículas de espín 1/2 que se hallan en un estado inicial:
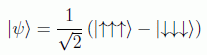
Y se considera el observable(3):
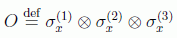
Es claro que los observables "parciales" σx ⊗ I ⊗ I, I ⊗ σx ⊗ I y I ⊗ I ⊗ σx pueden adoptar cualesquiera de sus valores espectrales (-1,+1) en mediciones independientes efectuadas en respectivas regiones causalmente separadas. Sin embargo, el observable conjunto O adopta siempre el valor -1:
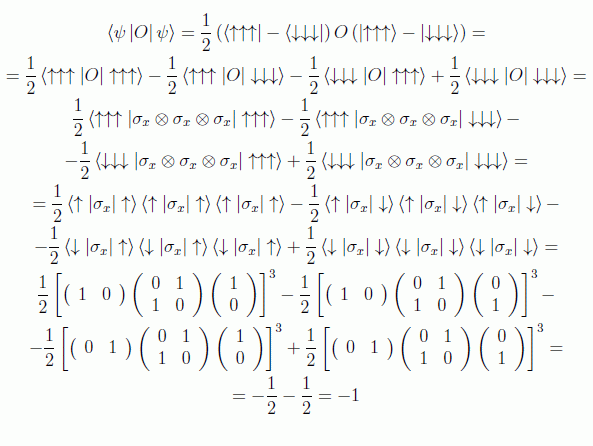
Pero además, la dispersión es nula (es decir, no solo el valor promedio de O es -1, sino lo hace con dispersión nula, o en otras palabras, la medición de O siempre da -1 para estados preparados en GHZ):
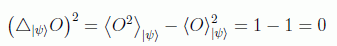
ya que
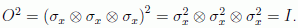
Las partículas presentan, por tanto, correlaciones exactas a tres. Dicho de otra manera: si una de ellas tiene σx=+1, y la segunda tiene σx=+1, la tercera no puede dar otro resultado que σx=-1 (y todas las demás variaciones obvias). No se puede obtener cualquiera de entre las 23=8 variaciones independientes de los resultados básicos { ±1,±1,±1} como posibles resultados del experimento, sino únicamente una de entre 2x2x1=4 posibilidades. Esquemáticamente:
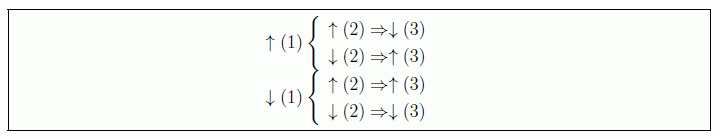
La moraleja de GHZ es que para que las partículas presenten estas correlaciones exactas a distancia, cualquier sistema de variables ocultas que lo explique debe violar la causalidad. Esa es la reivindicación de los que apelan al argumento GHZ, en cualquier caso.
(1) (Clauser-Horne-Shimony-Holt-Bell)
(2) La versión original de la desigualdad de Bell,
también llamada
desigualdad
de Clauser-Horne-Shimony-Holt, es 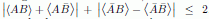 . La versión que
demostramos aquí es algo más sencilla e ilustra todos
los aspectos que nos interesan.
. La versión que
demostramos aquí es algo más sencilla e ilustra todos
los aspectos que nos interesan.
(3) Véase el blog de Jose Usera para una discusión sobre este asunto.