
PRINCIPIO DE INCERTIDUMBRE

En los orígenes de la Mecánica Cuántica, poco después de que Schrödinger publicara su interpretación ondulatoria de la misma, el debate seguía siendo si se podrían deducir de la teoría trayectorias u órbitas determinadas para las partículas subatómicas, tal como parecían ser ''observadas'' en las llamadas cámaras de Wilson desarrolladas una década antes. Eran días de debate entre el formalismo matricial y el ondulatorio, días en donde Bohr estaba dando forma a su famoso principio de complementariedad y mantenía interesantísimas discusiones al respecto con Schrödinger. Cabe destacar que aunque en aquel momento la mecánica matricial defendida por el alemán Werner Karl Heisenberg parecía imponerse sobre la ondulatoria de Schrödinger, hoy en día los dos formalismos aparecen como complementarios, en la llamada teoría de las transformaciones, desarrollada independientemente por Pascual Jordan y Paul Dirac, en donde se estudian las conocidas imágenes de evolución temporal de Heisenberg y Schrödinger, según el caso. Como nota anecdótica vamos a incluir una cita de Heisenberg en una carta a Pauli el 8 de junio de 1926, en los tiempos en los que era más crítico con la visión de Schrödinger:
''cuanto más pienso en los aspectos físicos de la teoría de Schrödinger, más repulsiva me parece... Lo que Schrödinger dice de la visualización de su teoría 'no es probablemente cierto del todo',(alusión a un comentario de Bohr) en otras palabras: es una mierda''.
En este escenario Heisenberg publicó en 1927 en la revista Zeitschrift für Physik (''Diario de Física'') uno de los artículos principales para entender los fundamentos de la Mecánica Cuántica, Über den auschaulichen Inhalt der quantentheoretischen Kinematic und Mechanik (''Sobre el contenido ideológico de la cinemática y la mecánica cuántica teórica''), que parecía dar un espaldarazo a las teorías de Bohr y sentar las bases de la conocida interpretación de Copenhague.
No obstante, aunque se puede decir que las visiones de Bohr y Heisenberg salieron claramente victoriosas de aquel debate (Schrödinger nunca aceptó los ''saltos cuánticos'' y las discontinuidades que al final se impusieron), hoy en día también es aceptado el hecho de que la ecuación de Schrödinger y su función de onda tienen mayor calado teórico que las relaciones de indeterminación que se pueden deducir de ciertas derivaciones del formalismo (a pesar de que ambos conceptos siguen apareciendo como postulados en muchos libros de Cuántica).
Aunque no es la derivación que hoy en día se puede encontrar en los libros de texto, vamos a recordar cuál fue el razonamiento original de Heisenberg en 1927. Para empezar él supuso el siguiente paquete de ondas gaussiano para la función de onda:
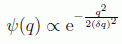
introduciendo la indeterminación δ q de la posición de la partícula y obviando los factores de normalización. De esta forma se puede deducir utilizando la transformada de Fourier cuál es el aspecto que tendrá la correspondiente incertidumbre en el momento, calculando:
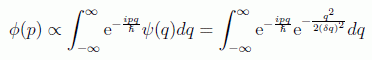
Para poder integrar con facilidad es conveniente completar el cuadrado que sugieren los exponentes exponenciales, es decir, utilizar la igualdad:
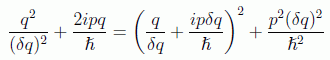
con lo que:
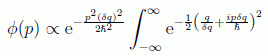
que es de inmediata integración haciendo el cambio:
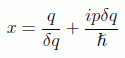
con lo que se puede decir simplemente, obviando de nuevo las constantes, que
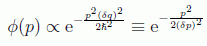
y el producto de las indeterminaciones será por tanto:
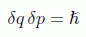
Aquí hay un problema. Esta expresión no nos suena del todo familiar. El hecho es que normalmente el principio de incertidumbre es enunciado a partir de las desviaciones estándar de las distribuciones de probabilidad, no a partir de las desviaciones de las funciones de onda, como se define en la ecuación propuesta . Como según la interpretación probabilística de Born la distribución de probabilidad nos la da el cuadrado de la función de onda, es obvio que las dos desviaciones están relacionadas con la fórmula:
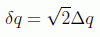
llegando, ahora sí, a la conocida expresión del producto de las desviaciones de la probabilidad:
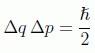
En el capítulo de la ecuación de Schrödinger vimos que en representación de posición los operadores posición y momento sobre el espacio de Hilbert L2(R) (funciones reales de cuadrado integrable) podían asociarse al llamado par de Schrödinger:

De aquí es fácil deducir las relaciones de conmutación que deben cumplir estos observables, llamada cuantificación canónica:
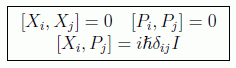
Hay que hacer notar que la tercera relación no podría realizarse con matrices finitas, dado que entonces Tr[A,B]=0 (y la traza de la identidad, obviamente, es no nula), pero sí se cumple en un par de Schrödinger como el apuntado arriba, y en general para cualquier par en donde alguno de los operadores sea no-acotado.
La exposición moderna del principio de incertidumbre se basa en el trabajo de Howard Percy Robertson, en el que se establece que el producto de las desviaciones estándar de dos operadores hermíticos A y B nunca será menor que la mitad del valor absoluto de la media de su conmutador, esto es,
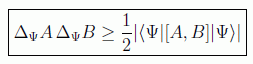
y el mismo Schrödinger hizo importantes contribuciones en esta línea de argumentación.
Recordemos que la desviación estándar se define como
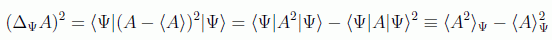
Se comienza suponiendo la siguiente forma para el valor medio del producto de dos operadores hermíticos C y D (y por tanto los valores medios de sus conmutadores y anticonmutadores):
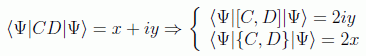
y por tanto
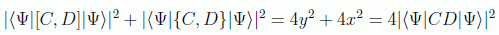
con lo que se puede decir que
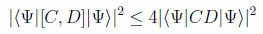
Sólo queda echar mano de la conocida desigualdad de Cauchy-Schwarz, cierta en espacios vectoriales normados, que afirma:
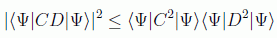
con lo que se tiene
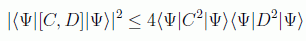
Redefiniendo los operadores como:
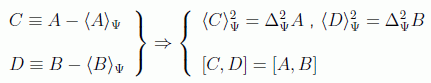
se llega a la desigualdad que se pretendía demostrar:
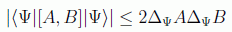
En el caso del momento y la posición en una dirección, utilizando las relaciones de conmutación vistas, se llega a la expresión ya conocida:
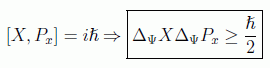
Si nos atenemos a las fórmulas obtenidas, las relaciones de indeterminación nos indican que es imposible diseñar experimentos de forma que se puedan medir, en sistemas preparados de igual forma, dos observables A y B con resultados de dispersión cuadrática media tan pequeña como se quiera para ambos, a no ser que [A,B]=0.
Si vamos más allá, y el propio Heisenberg lo hizo, se puede analizar que este hecho es consecuencia del propio proceso de medición, es decir, de la naturaleza de la interacción entre el sistema y el dispositivo de medida, pero hay que tener claro que el principio es una propiedad de la Naturaleza, es decir, no depende de las precisiones que se puedan obtener con distintos dispositivos. El principio de incertidumbre no restringe las precisiones que se pueden obtener sobre los observables. Lo único que afirma, siguiendo la interpretación que dio K.R.Popper en 1934 (más precisa que la del propio Heisenberg) es que existe una correlación estadística entre las desviaciones estándar que se pueden obtener en un conjunto de experimentos. Nada prohíbe, por ejemplo, que podamos conocer exactamente la cantidad de movimiento de una partícula en una dirección con total exactitud, siempre que paguemos el precio de haber perdido toda información acerca de la coordenada correspondiente de la posición de esa partícula, que quedará en este caso totalmente indeterminada. Como demostró el propio Heisenberg, la forma que debe tener la función de onda para que esta incertidumbre sea mínima es precisamente la dada por la gaussiana que supuso, ya que en este caso el principio satura la desigualdad, por eso debido a esto a veces se le llama paquete mínimo.
Hay también que hacer notar que este principio es válido para sistemas macroscópicos igualmente, aunque en este caso el fenómeno no sea observado. El movimiento de la luna también es perturbado por la medición, pero su masa es tan grande que la perturbación se puede ignorar. Una vez más, la pequeñez de la constante de Planck h es lo que pone el fenómeno fuera de las experiencias ordinarias. Esto tiene implicaciones filosóficas fundamentales, ya que si admitimos una ley de la naturaleza que restringe el conocimiento exacto de la posición y el momento iniciales de un sistema, no se podrá determinar con precisión su comportamiento en el futuro. Se pone en duda el determinismo en Física y, lógicamente, el propio concepto de trayectoria.
Para dar datos numéricos, supongamos que queremos conocer la trayectoria de un electrón en un átomo de hidrógeno. Lógicamente tendremos que determinar para ello significativamente su posición, en un átomo que recordemos que tiene un diámetro del orden del ångström (10-10m), con lo que intentaremos una precisión de digamos dos órdenes de magnitud menor, es decir:
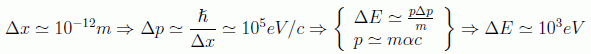
en donde α es la constante de estructura fina y m la masa del electrón. Esa dispersión en la energía obtenida es del orden de cien veces la energía de ionización del átomo y, por tanto, al intentar hallar la posición casi con toda seguridad lo ionizaremos y seremos incapaces de seguir la trayectoria del electrón.
Se puede establecer otra relación de incertidumbre derivada de nuestro principio sin más que considerar el caso de una partícula libre, un electrón por ejemplo, moviéndose a lo largo del eje x:
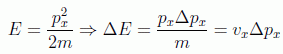
en donde esa velocidad que aparece se puede interpretar como la velocidad de retroceso del electrón cuando es iluminado para medir su posición. Por tanto podemos pensar que si la medida se realiza en un tiempo Δ t su posición también tendrá una incertidumbre dada por
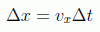
que combinada con la anterior nos da el llamado principio de incertidumbre energía-tiempo:
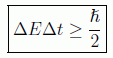
En general se puede decir, según vimos en un apartado anterior:
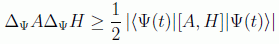
y teniendo en cuenta la evolución de los valores esperados se tiene
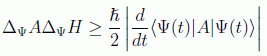
Por tanto, podemos interpretar el tiempo
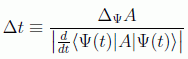
como aquel en el cual el valor esperado de A se desplaza una desviación estándar. Lógicamente, si A es una constante del movimiento este tiempo es infinito, al igual que si nos encontramos en un estado estacionario (en ambos casos las distribuciones de probabilidad no varían).