
EL LÍMITE CLÁSICO

Desde los inicios de la mecánica cuántica, uno de los temas de más controversia fue la falta de capacidad de esta teoría para predecir las trayectorias que pudieran seguir los sistemas individuales más simples.
Los fundadores de la cuántica rápidamente vieron que su paso al límite clásico no era tan fácil como suponer ћ→0, como lo era en el caso de la mecánica relativista respecto a la newtoniana, en donde con el simple límite c→∞ se recuperaba el formalismo clásico.
La razón de esta complejidad en el caso cuántico se basa en que la teoría es en esencia de naturaleza diferente de la teoría clásica. En efecto, tanto la mecánica relativista como la newtoniana se basan en la admisión de trayectorias continuas individuales de las partículas en el espacio-tiempo, mientras que la mecánica cuántica está formulada en términos de probabilidades. Esta diferencia cualitativa es mucho más difícil de salvar con un simple límite.
De aquí se deduce que el límite ћ→0 es necesario, pero no suficiente. No esperemos recuperar una trayectoria clásica cuando se dé ese límite , más bien fijémonos en las distribuciones de probabilidad que nos da el formalismo y estudiemos su equivalencia con el conjunto de distribuciones de probabilidad de las trayectorias clásicas correspondientes. Esta sería la forma más correcta de proceder en el límite.
Vamos a estudiar aquí algunos de los intentos por dar interpretaciones clásicas al mágico mundo de las trayectorias cuánticas, empezando por la del malogrado Paul Ehrenfest.
El primer camino para la recuperación de la imagen clásica lo siguió Ehrenfest en 1927 (artículos), y se basa en atribuir a cada partícula unas coordenadas y momentos que fueran precisamente los valores medios calculados en su estado. Para que este camino se pudiera seguir era necesario, lógicamente, que los valores medios cumplieran las ecuaciones clásicas del movimiento.
Recordemos que para una hamiltoniana clásica como
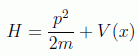
las ecuaciones del movimiento eran
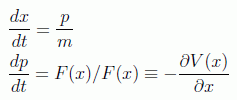
Pasando al caso cuántico, y suponiendo que se trata de un sistema aislado en donde los observables no dependen explícitamente del tiempo, en imagen de Heisenberg teníamos la evolución operacional:
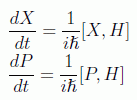
Los corchetes los calculamos con el hamiltoniano correspondiente quedando:
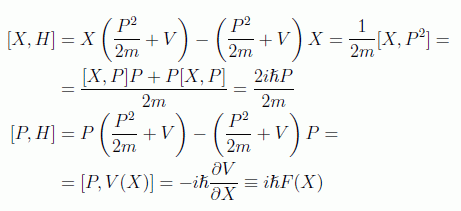
en donde se ha usado la igualdad
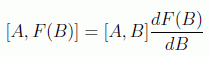
Por tanto, tomando medias en algún estado llegamos al teorema de Ehrenfest:
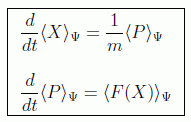
lo que demuestra que los valores medios satisfacen las leyes clásicas siempre que admitamos definir una fuerza media cuyo conocimiento depende de la función de onda. Lógicamente esta fuerza media no tendrá una expresión equivalente a la clásica con respecto a la posición media a menos que funcione la aproximación:
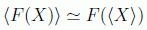
Si hacemos un desarrollo en torno a < X > observamos:
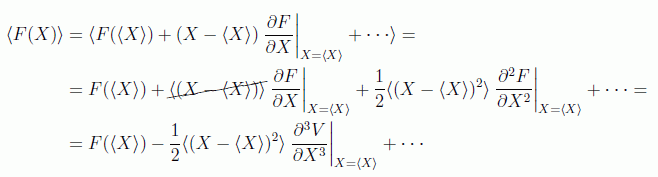
con lo que el teorema de Ehrenfest predice que los valores medios se mueven con las ecuaciones clásicas del movimiento siempre que V(X) dependa a lo sumo cuadráticamente de X, lo que en efecto ocurre para casos como la partícula libre o el oscilador armónico.
Desgraciadamente con esto se ve que el teorema de Ehrenfest no es suficiente para definir un régimen clásico, ya que como hemos visto el oscilador armónico lo cumple y sin embargo es un sistema claramente cuantificado. Lo peor sin embargo es que tampoco es necesario, ya que un sistema puede comportarse clásicamente y no cumplir el teorema, debido al comportamiento similar que tienen las distribuciones de probabilidad clásicas.
Si imaginamos una partícula libre en una dimensión que en un instante determinado se encuentra localizada en un lugar con una distribución gaussiana de probabilidad del tipo

El valor de la varianza en posición para la distribución de probabilidad correspondiente deberá ser lógicamente a/2, pero vamos a comprobar esta y la correspondiente al momento.
Debemos antes admitir los dos resultados siguientes para las integraciones de gaussianas (no son difíciles de demostrar haciendo una extensión al plano y utilizando polares):
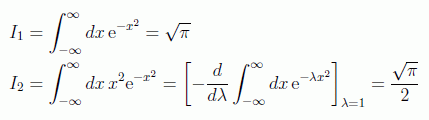
Vamos a obviar por comodidad los límites de integración a partir de ahora, si hacemos los cálculos:
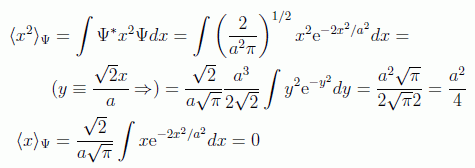
en donde la última integral se anula por ser una función impar en intervalo simétrico, llegamos a

Y en el caso del momento:
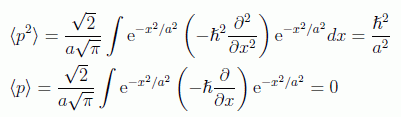
con lo que
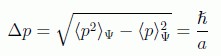
Y por tanto en el caso de la gaussiana, como ya vimos en la dedución de Heisenberg del principio de incertidumbre, la desigualdad entre sus productos se satura, es decir, se convierte en estricta igualdad:
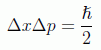
de ahí que como vimos sea conocida esta función con el nombre de paquete mínimo. Ahora vamos a comprobar que, aunque este paquete mínimo se conserva a lo largo del tiempo, las incertidumbres sin embargo evolucionan. Para ello debemos calcular la evolución de la función de onda vía ecuación de Schrödinger, que puede tener un desarrollo en el espacio de momentos del tipo:
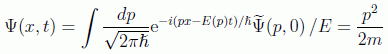
en donde debemos calcular la transformada de Fourier
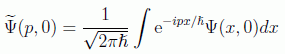
que podemos hallar sustituyendo la expresión de la función de partida y calculando por integración gaussiana gracias al artificio de completar el cuadrado
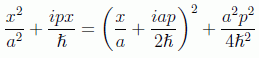
obteniendo


De esta forma podemos sustituir en la expresión de la función de onda dependiente del tiempo y, tras un prolijo cálculo en donde de nuevo habrá que completar el cuadrado, se obtiene:
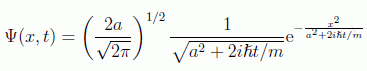
y para la evolución buscada de las incertidumbres el resultado:
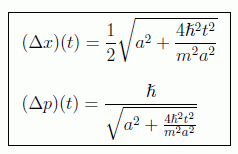
en donde se puede apreciar que si dejamos la evolución libre la partícula acabará totalmente deslocalizada con un momento definido al igual que ocurría en el caso de una onda plana (figura).
Vamos a estudiar la evolución de las incertidumbres en el caso más general de la partícula sometida a un potencial a lo sumo cuadrático respecto a sus coordenadas, suponiendo sin pérdida de generalidad de nuevo el caso unidimensional. Veremos de nuevo que en alguno de los casos se dará la dispersión total del paquete de ondas aunque en efecto sea válido el teorema de Ehrenfest y de aquí deduciremos lógicamente que para que un sistema se pueda comparar con uno clásico no es suficiente aceptar el teorema de Ehrenfest sino que se debe cumplir mejor que las dimensiones del paquete sean despreciables en comparación con las dimensiones que caractericen el problema.
Vamos antes de nada a admitir el hamiltoniano:
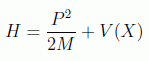
y asumir que en principio este no nos dará en su valor medio la energía esperable clásicamente, es decir:
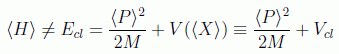
como ambas son constantes del movimiento es claro que su diferencia también será constante:
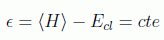
Y también suponemos que el potencial tiene un desarrollo convergente que en el caso de un potencial a lo sumo cuadrático se expresa en la forma:
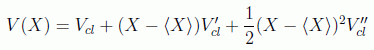
Vamos a partir de estas premisas para calcular la evolución temporal de las incertidumbres, o más fácilmente de sus varianzas, denotadas aquí como:

con lo que se tiene
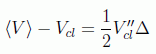
y por tanto la constante queda

Vamos a buscar una forma simple para la evolución temporal:
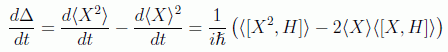
Y en consecuencia debemos calcular los conmutadores:

con lo que
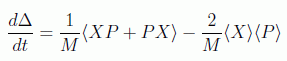
La segunda derivada será
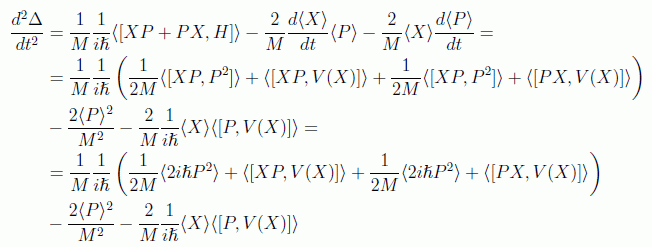
que podemos abreviar usando igualdades como
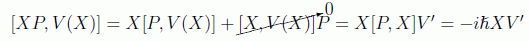
quedando
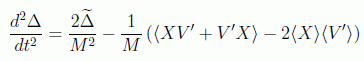
y recordando que en aproximación cuadrática tenemos
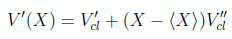
obtenemos la expresión
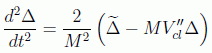
Para quitar la varianza en el momento de esta expresión recurrimos a la fórmula de la constante que representaba la diferencia en energías. Consiguiendo por fin:
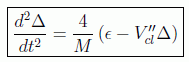
Lo que indica que, como era de esperar, la diferencia de energías clásica y cuántica está asociada a las fluctuaciones de la posición de la partícula respecto de su posición clásica.
A partir de esta ecuación se pueden estudiar casos sencillos de potencial y ver la expresión de su varianza (Messiah, Galindo/Pascual) a partir de las condiciones iniciales, que normalmente están asociadas a una gaussiana (paquete mínimo). Así se ve que en el caso de una partícula sometida a una fuerza constante (potencial lineal) los paquetes se ensanchan como en el caso libre o que en el caso de un potencial armónico (potencial cuadrático) curiosamente el paquete no llega nunca a desbocarse ya que la dependencia que sale es sinusoidal.
Ya hemos estudiado la evolución de un paquete mínimo o gaussiano de forma libre y las soluciones de la ecuación de Schrödinger en los casos más simples, pero ahora vamos a adoptar el punto de vista más general que se relaciona con la evolución de los paquetes de onda mediante el concepto de propagador o función de Green. Nos enmarcamos pues en una pequeña introducción a la teoría de la difusión o de colisiones, que básicamente es la dispersión de la onda por potenciales perturbativos y sus posibles aproximaciones. Ahora la ecuación diferencial de Schrödinger y su condición inicial serán sustituidas por ecuaciones integrales. En esto consisten los métodos variacionales propuestos por Bernard A. Lippmann y Julian Schwinger en 1950, herederos en cierta medida de la semilla puesta por John Archibald Wheeler en 1937 en donde se introdujo el paradigma de la matriz S.
Según esta teoría la función de onda dispersada por un potencial V(x) desde un punto (x1, t1) a un punto (x2,t2) debe cumplir una ecuación integral en donde el estado inicial es perturbado para dar lugar a un estado final modificado en donde la dinámica se hace recaer en el propagador retardado K:

que deberá cumplir la ecuación de Schrödinger junto con la condición causal:
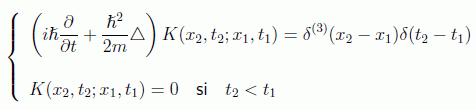
Esta metodología es susceptible así de iterarse indefinidamente encontrando algo parecido al principio de Huygens, es decir, cada frente de onda es fuente de frentes de onda y el total en un punto se obtiene sumando todas las contribuciones:
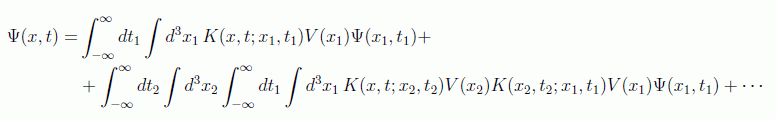
a este tipo de series se las denomina series de Born y tienen una interpretación clara. La onda inicial en (x1, t1) sufre la acción del potencial en x1 y llega a (x,t) y a (x2, t2), en donde sufre la acción del potencial en x2 y llega a (x,t) y llegará a (x3, t3), etc.
Para resolver la ecuación para K hay que recordar que
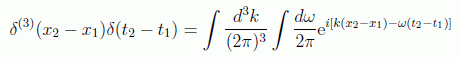
por tanto, si uno supone la expansión en ondas planas:
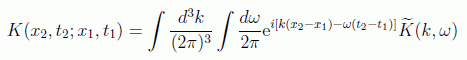
se obtiene la expresión
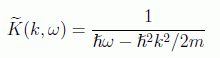
Para salvar la divergencia provocada en el denominador al integrar se utiliza el artificio de poner una cantidad imaginaria de modo que tienda a cero después de realizar la integración compleja:
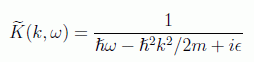
y realizar la integral por residuos
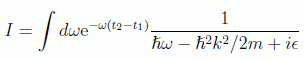
en el circuito propuesto en el plano ω de la figura
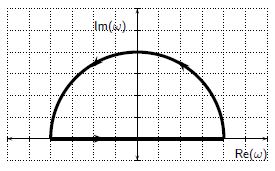
Dentro del circuito no hay polos, al estar este en

y esto nos asegura la condición de causalidad propuesta, ya que

cuando hacemos tender el circuito a infinito y aplicamos el teorema del residuo. Esto implica que K se anula si el tiempo inicial es mayor que el final y la elección hecha de la forma del propagador es la correcta.
Como la onda inicial suele ser plana, se suele admitir la factorización en parte espacial y temporal, y usar el propagador también factorizado en la forma:
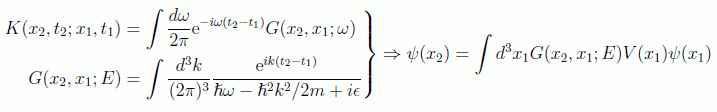
en donde se han intercambiado las dependencias en la frecuencia o de la energía por ser estas equivalentes. Esta es la conocida como ecuación integral de Lippmann-Schwinger. Se puede ahora evaluar la parte del propagador espacial (función de Green) si integramos en el espacio de $k$ con la dirección del eje z coincidiendo con x2-x1. El elemento de volumen será

con lo que la integración de la parte angular es inmediata y dará:
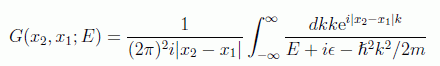
en donde los polos en este caso son:
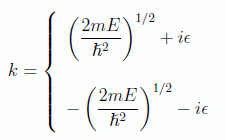
y por tanto, integrando por residuos en un circuito análogo al anterior, teniendo en cuenta el límite:
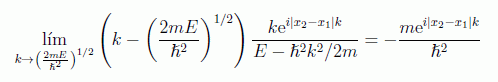
se obtiene
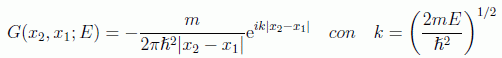
Por tanto, a grandes distancias la onda dispersada se ve como una onda saliente con simetría esférica. La amplitud de la onda es el objeto de estudio de la teoría de la dispersión y según las aproximaciones y los potenciales que estudiemos nos dará distintas expresiones para las secciones eficaces (que al fin y al cabo será el dato físico por excelencia).