
INTRODUCCIÓN A LAS TEORÍAS CUÁNTICAS DE CAMPOS

Toda teoría respetable sobre las partículas elementales se desarrolla dentro del marco de la teoría cuántica de campos (TCC o, en inglés, QFT), que amplió la Mecánica Cuántica (QM). Aquí se pueden encontrar la electrodinámica cuántica, el modelo estándar, la teoría de supercuerdas, etc.
Estas teorías deben respetar tres principios fundamentales:
i) La validez de la Mecánica Cuántica.
ii) La validez de la Relatividad.
iii) La localidad. Esto implica que todas las fuerzas surgen de procesos locales, no de acción a distancia.
De aquí se derivan dos consecuencias que van a caracterizar siempre este tipo de teorías:
1) El número de partículas en las interacciones no es conservado, ni tampoco la clase o tipo de las partículas implicadas. Pueden desaparecer unas y aparecer otras, del mismo o distinto tipo, ya que los procesos locales incluyen la emisión y absorción de partículas.
2) Existe una simetría fundamental entre las partículas elementales y sus antipartículas. Para cada partícula hay una antipartícula correspondiente, que se comporta moviéndose hacia atrás en el espacio y en el tiempo, y posee carga eléctrica opuesta. Algunas partículas neutras son antipartículas de sí mismas.
Existen al menos dos formas de aproximarse a la QFT, por medio de las cuantizaciones canónicas, o por medio de la llamada integral de camino (también llamada suma sobre historias). Empezaremos en estos apuntes por la primera opción, ya que es la que deviene naturalmente del curso histórico de la QM.
En el marco de la QM no hay manera de tratar procesos de transformación de una partícula en otras o de interacciones entre partículas dando lugar a otras partículas, ya que se trata de una teoría que asume que las partículas conservan su identidad e integridad.
En QFT podemos sin embargo estudiar procesos de aniquilación y creación de partículas, que pueden suceder con intercambio de las llamadas partículas virtuales, hallando lo que se conoce como amplitudes de transición, que nos darán la probabilidad que posee cada suceso de ocurrir en la práctica.
Otro punto, relacionado con el anterior, que ocurre cuando estudiamos procesos en el rango en donde empieza a ser apreciable la relación energía-masa relativista, es que hay que estudiarlos con una teoría cuántica relativista que tenga en cuenta estas transformaciones, y la QM no cumple este requisito.
Veremos que los intentos de hacer una Mecánica Cuántica Relativista (RQM) llevaron a los físicos a muchos problemas de interpretación, debido a que aparecían energías negativas que no se podían desechar por la limitaciones impuestas por el principio de incertidumbre, que toma una dimensión más dramática cuando se combina con la relatividad.
Cuando introducimos el principio de relatividad en las ecuaciones de la Mecánica Cuántica, añadimos limitaciones a las posiciones con las que se pueden conocer los observables físicos. Recordemos el principio de indeterminación de Heisenberg en su forma más grosera:
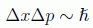
En principio, como ya dijimos en su momento, no nos ponía ninguna restricción a la precisión con la que se puede medir cada uno de los observables por separado. Sin embargo, si lo leemos en función de una diferencia de velocidades antes y después de la medición:
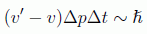
es claro que, dada la existencia de una velocidad límite c en Relatividad Restringida, la diferencia entre las dos velocidades jamás podrá ser mayor que 2c, con lo que:
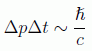
dándonos una máxima precisión alcanzable para la medida del momento en un intervalo temporal de medición Δ t. esta imprecisión se puede trasladar también a la medida de la posición de la partícula, y está íntimamente relacionada con la aparición de nuevas partículas en el proceso de medición, como en el caso de la formación de pares.
El intento de solventar estas dificultades fue lo que llevó a físicos como Paul Dirac, Vladímir Fok o Wolfgang Pauli a crear la Teoría Cuántica de Campos. En ella las funciones de onda adquieren el rango de operadores capaces de destruir y crear nuevas partículas, y se añaden por tanto a las relaciones de conmutación de los observables nuevas relaciones de conmutación de los estados, por ello en muchas ocasiones se le ha llamado formalismo de segunda cuantificación , un término realmente desacertado y desorientador, dado que de hecho no se produce ninguna segunda cuantificación a nivel físico.
En este escenario, realmente las únicas magnitudes observables serán las de las partículas libres: las de las iniciales que entran en la interacción y las finales que aparecen como resultado del proceso de medición. El conjunto de las amplitudes de todos los estados posibles formará la llamada matriz de dispersión o matriz S, portadora de la verdadera información con sentido físico.
Las dimensiones de las magnitudes no tienen características fundamentales. Son útiles para asegurar la coherencia de una ecuación física comprobando que no se están igualando magnitudes diferentes por medio del análisis dimensional y para relacionar unidades de la misma magnitud.
Podemos admitir, por ejemplo, que las magnitudes mecánicas longitud (L), masa (M) y tiempo (T) son las dimensiones fundamentales. Pero en el Sistema Internacional (SI), por ejemplo, se añade una unidad independiente de carga (Q) suponiendo para la ley de Coulomb la forma:
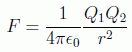
suponiendo que la constante de Coulomb tiene dimensiones. Sin embargo uno puede forzar que las cargas se puedan expresar en unidades mecánicas admitiendo los siguientes sistemas de unidades:
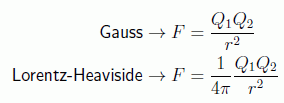
en donde el último, llamado racionalizado porque en las ecuaciones no aparece el término 4π, es el más usado en teorías cuánticas de campos.
Aparte, en teorías cuánticas de campos, debido a los principios de relatividad y de incertidumbre, se suelen utilizar las unidades naturales, en donde las constantes de Planck y de la velocidad de la luz, con los valores en el SI:
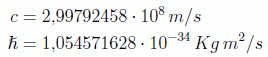
se escogen como unidades de acción y de velocidad respectivamente:
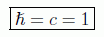
Hay que decir también que dentro de las unidades naturales se pueden usar otras más restrictivas llamadas unidades geometrizadas o de Planck, en donde todas las magnitudes se pueden expresar con números adimensionales, haciendo:
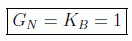
es decir, igualando a la unidad la constante gravitacional de Newton y la constante de Boltzmann. En QFT sin embargo no se suelen incluir debido a que la gravitación no afecta a las ecuaciones.
Las unidades naturales tienen la ventaja de que todas las magnitudes las podemos expresar en términos de energía, y para ésta se suele escoger como unidad el electronvoltio (eV) ya que es una unidad más adecuada para el mundo microscópico:
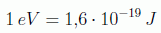
Por ejemplo, la energía de un protón en julios es

sin embargo vemos que es aproximadamente un gigaelectronvoltio:
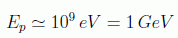
siendo la del electrón unas 2000 veces menor, es decir, medio megaelectronvoltio:
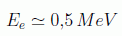
Teniendo en cuenta las dimensiones de las constantes naturales podemos deducir que, por ejemplo, el tiempo y la longitud tienen las mismas unidades, y son equivalentes a las de la inversa de una masa o energía:
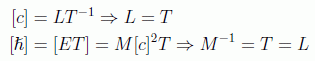
En estas unidades identificamos por tanto la energía con la masa o la frecuencia según el caso, así como el momento con el número de onda, ya que:
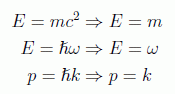
y esta última magnitud se podrá medir también en electronvoltios:
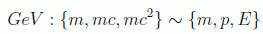
Asimismo la longitud y el tiempo tendrán dimensiones de inversa de energía, como podemos ver si suponemos un fotón atrapado en una caja de tamaño L, que por el principio de incertidumbre cumplirá:
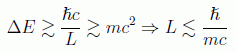
en donde se ha impuesto la energía umbral capaz de dar lugar a nuevas partículas vía principio de incertidumbre. Es por eso que la llamada longitud de onda Compton:
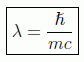
es la típica en donde se dan los procesos de QFT y se mide en unidades de inversa de energía:
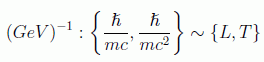
Para un protón (neutrón) por ejemplo tenemos la equivalencia:

es decir, del orden de la décima parte de un femtómetro (fm), que es precisamente la unidad que marca los diámetros de los nucleones.
Otras equivalencias con el SI que se pueden deducir fácilmente son:
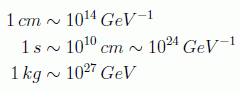
Las dimensiones de la constante de Newton de la Gravitación son, recordando la definición de su energía potencial:
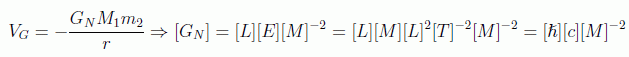
y en unidades naturales tendrá las dimensiones de una masa/energía a la -2 o equivalentemente de una longitud al cuadrado. Esto sugiere definir una escala natural de masas, longitudes y tiempos:
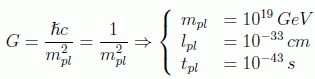
conocida como escala de Planck. Para longitudes menores que la de Planck no hay una teoría satisfactoria, dado que empieza a tener influencia la gravedad cuántica. En el otro extremo de distancias tenemos el horizonte cosmológico:
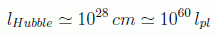
Eso en cuanto a las escalas extremas de longitudes, vamos a ver ahora la escala de intensidades de las diferentes fuerzas. Como la constante cosmológica tiene dimensiones es difícil calcular la intensidad para compararla con las demás fuerzas. Sin embargo podemos hacernos idea de la debilidad de la gravitación con la combinación adimensional con la masa del protón:
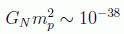
Si se hace un cálculo análogo con la constante de acoplo de Fermi, que nos da idea de la intensidad de la fuerza débil, se obtiene:
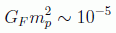
y por tanto la interacción débil es aproximadamente 32 órdenes de magnitud más fuerte que la gravedad, lo que define el llamado problema de jerarquía en Física Teórica.
Asimismo podemos hacernos una idea de la intensidad de la fuerza electromagnética por medio de otra cantidad adimensional: la constante de estructura fina. Si en las unidades de Heaviside calculamos la razón entre la energía electrostática a una distancia Compton y la total de una partícula de carga elemental tenemos la mencionada constante:
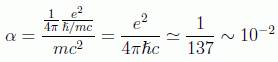
Como detalle de este cálculo veamos la equivalencia de las unidades de carga con el SI:
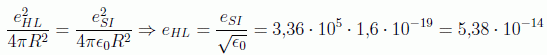
con lo que
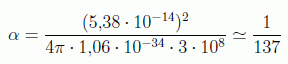
Para la fuerza nuclear fuerte también se puede calcular un orden de magnitud a través de su constante de acoplo adimensional, obteniendo:
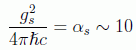

Vamos a hacernos por último una idea de las escalas energéticas que están en juego por medio de la siguiente tabla:

El alcance energético que se espera conseguir en los últimos experimentos, como el LHC del CERN , es el del TeV, en donde se esperan descubrir los últimos ingredientes del modelo estándar, en particular el bosón de Higgs. Cuando se escriben estas líneas se están produciendo colisiones de varios TeV, pero éstas deben ser convenientemente analizadas todavía. Para hacernos una idea veamos algunas de las masas de las partículas en juego:
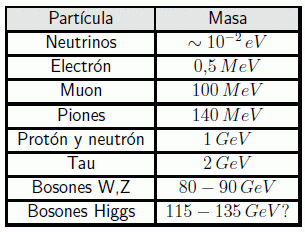
Recordemos un hecho fundamental, la introducción del concepto de campo, tanto clásica como cuánticamente, viene dictada por razones de invariancia relativista. En este sentido el concepto de campo surge de manera natural al negar la idea de acción instantánea y a distancia de una partícula sobre la otra. Suponiendo que el espacio está ocupado por el campo hacemos respondable a este de la transmisión de las excitaciones.
El concepto de campo cuántico es una síntesis de los de campo clásico de tipo electromagnético y función de onda de probabilidad de la QM. Las ondas en este contexto se van a estudiar como colecciones de osciladores armónicos relacionados con sus distintas frecuencias. Normalmente se estudia de inicio un sistema discreto en representación de momentos, pasando después al continuo.
Si suponemos para simplificar una sola dimensión periódica de longitud L dividida en N partes, como una cuerda vibrante, de la teoría cuántica clásica del oscilador vimos que sólo estaban permitidas ciertas frecuencias (energías), que se harán corresponder con las contribuciones de cada grupo de osciladores en sus distintos modos de oscilación.

Como cada oscilador armónico tiene su energía cuantificada, podemos describir el campo cuántico con un vector que nos dé idea del número de cuántos que hay en cada estado del sistema (nivel energético) etiquetado aquí con i:
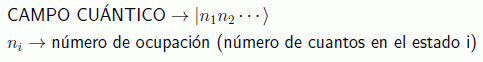
a este espacio se le denomina tradicionalmente espacio de Fok.
Yendo a una descripción más precisa podemos evaluar los momentos correspondientes a cada estado. En efecto, si suponemos una onda plana cada uno, la condición de periodicidad impuesta nos arroja los valores del momento:
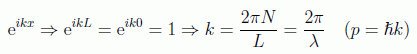
Para construir el estado total necesitamos de nuevo recurrir a la teoría clásica, los operadores de creación y destrucción, que serán las versiones mecanocuánticas de los coeficientes de Fourier y actuarán sobre cada estado (nivel, subespacio) y por tanto deberán ser etiquetados por la frecuencia (número de onda).
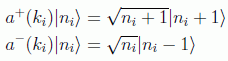
y serán los encargados de añadir o sustraer cuantos de energía.
De esta forma un proceso de dispersión en donde una partícula pasa de tener un momento k7 a uno k9 se puede describir como:
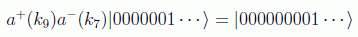
En representación de posiciones podemos suponer los siguientes desarrollos del campo:
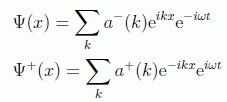
Se trata en este caso de operadores que definirán la forma de los estados correspondientes. El primero destruye una partícula en la posición x y el segundo la crea:
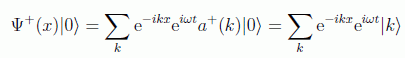
en donde k en el último caso no denota el número de ocupación sino el estado de una partícula con momento k, sumado a todos los posibles valores del momento que se puedan dar en esa posición.
Siguiendo con esta notación abreviada:
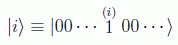
podemos analizar el proceso de dispersión de una a dos partículas producido por un átomo que se describe en la figura:
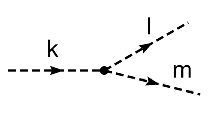
En este hipotético caso no hay conservación del momento, ya que no tenemos en cuenta el retroceso del átomo, pero se puede aventurar la siguiente forma para el estado final:
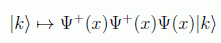
Aplicando nuestras expresiones:
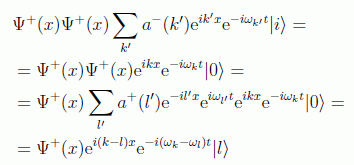
Ahora crearíamos la partícula en el estado de momento m, y aquí cabe hacer una distinción, si m=l (cosa que sólo se podría dar en el caso de bosones, como explicaremos más adelante) el resultado sería:
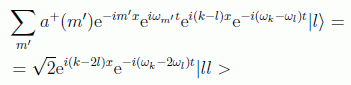
y en el caso de que los momentos salientes no coincidieran tendríamos, lógicamente
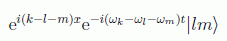
Vemos por tanto que el formalismo en principio siempre favorece la creación de partículas en el mismo estado, dado que la amplitud de ese resultado es mayor.
Supongamos un proceso de dispersión de una partícula en donde no fijamos el tiempo y vamos a calcular la amplitud del mismo:
La dispersión se produce en un sitio del espacio bien definido x=0. La amplitud de probabilidad puede ser de la forma:
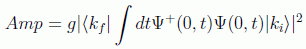
La fuerza de la interacción dependerá de la carga de la partícula y la asociamos con una constante de acoplo g. Este ejemplo vale para constantes pequeñas en donde no hay contribuciones de otros posibles procesos.
Desarrollando el cálculo obtenemos
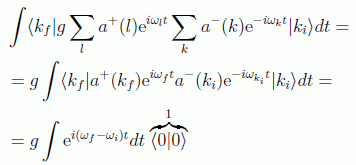
Aquí tenemos que recordar una propiedad de la delta de Dirac, que se puede "deducir" de su definición, que se muestra en la figura (recordemos que la delta de Dirac en el fondo no es una función sino una distribución matemática, así que los argumentos que daremos serán más bien heurísticos).
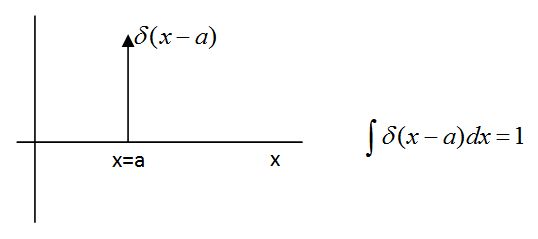
Como sabemos por otra parte por las propiedades de periodicidad se tiene:
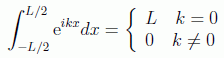
pero este resultado lo podemos interpretar como una función de k que vale L para k=0. Recordando en la figura la discretización de k podemos ver que como función de k definiría un área de 2π. De este modo como función de k vemos que se trata de una función que integrada nos da ese valor de 2π, con lo que en el paso al límite cuando L tiende a infinito y el intervalo a cero recuperaremos nuestra función delta multiplicada por esa constante, es decir:
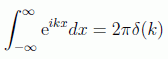
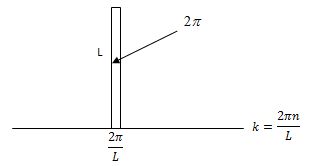
Aplicando esto a nuestro caso en el desarrollo que teníamos obtenemos:

lo que quiere decir que solo hay una cierta probabilidad cuando la energía se conserva, es decir:
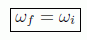
y la probabilidad tiene la forma:
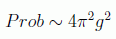
Hemos deducido por tanto la ley de conservación de la energía suponiendo una simetría de traslación temporal.
Por supuesto no hemos supuesto nada del momento saliente, que puede ser cualquiera compatible con la conservación de la energía. Si suponemos que el proceso puede ocurrir en cualquier punto del espacio, fijado un tiempo t=0 por comodidad, la integral la haremos sobre x y obtendremos la ley de conservación del momento:
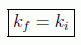
De la misma forma veremos que la conservación de la carga está ligada a la simetría de invariancia gauge definida por los cambios de fase:
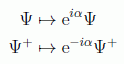
que básicamente se cumplirá si hay en los esquemas el mismo número de Ψ's que de Ψ+'s para cada tipo de partícula.
Las teorías cuánticas de campos hoy en día basan su fundamento en gran medida en las llamadas teorías de los campos de gauge1, que han sido desarrolladas en su forma general por muchos físicos a partir de mediados del siglo XX, gracias en parte a la semilla puesta por Chen Ning Yang y Robert Mills, que ampliaron trabajos anteriores de Kaluza, Klein, Fok y otros sobre el electromagnetismo y la gravitación (ambas teorías están mediadas por partículas no masivas).
Veremos que en el electromagnetismo la llamada simetría gauge tiene como consecuencia la conservación de la carga y que está asociada a una arbitrariedad en la expresión del potencial electromagnético. Pero recordemos antes la forma de las ecuaciones de Maxwell en unidades naturales de Heaviside-Lorentz:

De esa forma es conocido que las ecuaciones de Maxwell aparecen invariantes bajo el grupo SO(3) de rotaciones ya que si usamos la notación tensorial de 3 dimensiones:
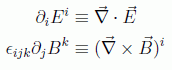
en donde εijk es el símbolo de Levi-Civita, completamente antisimétrico en sus tres índices, y cuyo valor es +1 si viene de una permutación par de (1,2,3) y -1 si no. Como es invariante bajo SO(3) queda por tanto manifiesta la invariancia de las ecuaciones de Maxwell así descritas bajo rotaciones:

No obstante, para conseguir covarianza bajo transformaciones de Lorentz SO(1,3) hay que recurrir al llamado tensor de Faraday, matriz antisimétrica 4x4, definida como:
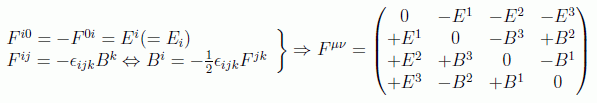
en donde la expresión del campo magnético en función del tensor de Faraday la hemos hallado usando la propiedad:
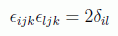
ya que
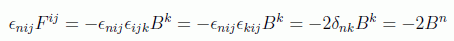
Además, usaremos la notación habitual para subir y bajar índices con la métrica (1,-1,-1,-1). Como ya entramos en un espacio tetradimensional las fuentes se agrupan en el cuadrivector:
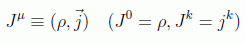
que cumple la ecuación de continuidad

usando las ecuaciones con fuentes, dado que la divergencia de un rotacional se anula.
En función de este nuevo tensor, veamos cómo quedan las ecuaciones de Maxwell. En cuanto a las dos primeras, las que poseen fuentes del campo, se tiene la correspondencia:
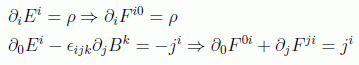
en donde se ha usado, aparte de la antisimetría del tensor de Faraday, la propiedad:
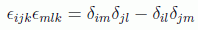
Y por tanto las ecuaciones de Maxwell con fuentes (inhomogéneas) se pueden abreviar como:
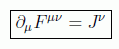
ya manifiestamente covariantes.
Con esta notación covariante la ecuación de continuidad es inmediata, ya que dos derivadas son simétricas (conmutan) y el tensor es antisimétrico, con lo que su contracción se anula, esto es:

En cuanto a las ecuaciones homogéneas o geométricas, se puede deducir de la primera:
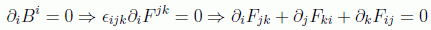
y de la última, con un cálculo más engorroso, obtenemos:

Los dos últimos resultados se pueden poner como
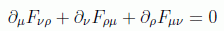
y usando el símbolo [μ ν ρ] de completa antisimetrización de índices, definido por:
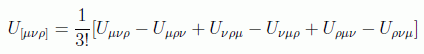
y teniendo en cuenta que el tensor de Faraday es antisimétrico, las ecuaciones homogéneas de Maxwell se pueden poner como
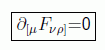
Estas ecuaciones se pueden resolver si introducimos el potencial cuadrivector:
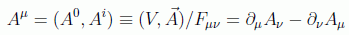
ya que las derivadas conmutan y la antisimetrización anula todos los términos. Los campos eléctrico y magnético en función de este vector se pueden poner como:
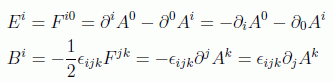
que identificando con los conceptos clásicos de potencial eléctrico y potencial vector conducen a las ecuaciones conocidas:

Sin embargo, se puede comprobar que el cuadripotencial Aμ no está unívocamente definido, ya que el tensor de Faraday (o los campos magnético y eléctrico) no cambian si se escoge otro cuadrivector que difiera del original en el gradiente de un campo escalar:
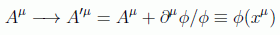
esta libertad se denomina transformación de gauge, y la invariancia de las ecuaciones de Maxwell respecto a ella se denomina invariancia gauge del electromagnetismo.
Esta arbitrariedad del cuadrivector se puede fijar de formas alternativas en lo que constituye la llamada elección del gauge, fijando tal o cual condición al mismo. Los más conocidos son:

aparte de que en un sistema general que contenga campos escalares se pueden incluir estos en la condición de gauge, como en el llamado gauge unitario.
Por ejemplo, en el gauge covariante de Lorentz, si hacemos:

es evidente que se puede fijar la función gauge φ sin más que imponer que su d'alambertiano se anule:
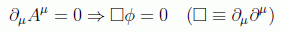
que siempre admitirá una solución para φ.
Con este gauge las ecuaciones dinámicas se simplifican considerablemente, ya que
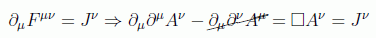
que constituye la conocida ecuación de ondas con fuentes.
Conviene hacer notar una cuestión acerca de esta simetría gauge. Puede parecer una simetría ficticia, derivada del empeño en expresar la dinámica en términos de este potencial, pero esto no es así. En la teoría cuántica efectos como el de Aharonov-Bohm muestran que los campos E y B no son suficientes para describir la interacción electromagnética con la materia, y es necesario añadir el potencial, que aquí adquiere un verdadero sentido físico. Los potenciales son necesarios para la cuantización de las partículas materiales y la propia cuantización de la interacción electromagnética.
1:Son muchos los intentos que se han hecho para traducir este término al castellano, y así podemos encontrar en la bibliografía las palabras contraste, patrón, calibre o aforo, esta última sugerida por Blas Cabrera. No obstante, la tendencia que se ha impuesto finalmente es la de dejar la palabra original.
Como ejemplo de paso a la segunda cuantificación vamos a seguir con el campo electromagnético. Veremos el procedimiento en el gauge de Coulomb ya que el de Lorentz exige más arsenal teórico. Esto es debido a que el gauge de Lorentz en principio es incompatible con las reglas de cuantificación y hay que suponer condiciones más débiles, normalmente usando el llamado método de Gupta-Bleuer. El precio que pagamos al elegir el gauge de Coulomb es la pérdida de la covariancia, pero en cambio ganaremos en claridad física en cuanto a la polarización de la luz, ya que permite quedarse sólo con los dos grados de libertad necesarios para describir ésta. Más adelante emplearemos el método general con el gauge covariante y las cuantificaciones canónicas.
Para empezar recordemos que en ausencia de fuentes las ecuaciones de Maxwell toman la forma:
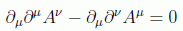
y si, como hemos dicho, admitimos el gauge de Coulomb:
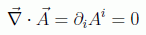
se pueden desglosar como:

De la primera de las ecuaciones averigüaríamos el potencial electrostático V, pero en ausencia de cargas se puede elegir nulo, lo que implica que la segunda de las anteriores ecuaciones quedará como la ecuación de ondas para cada componente del vector potencial electromagnético:
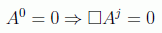
Podemos por tanto expandir las soluciones del potencial en series de Fourier dentro de una caja de dimensiones L1,L2 y L3 suponiendo condiciones periódicas para cada coordenada y obteniendo la conocida cuantificación en el espacio de momentos:

tendremos

en donde dejamos manifiesto el carácter real del campo.
Es manifiesto que en este espacio de momentos la condición de Coulomb se lee como una condición de transversalidad para cada componente:
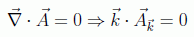
que también deberá satisfacer, sustituyendo en las ecuaciones del campo y usando su linealidad:
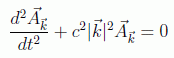
o, lo que es equivalente, cada componente del campo es solución de la ecuación de un oscilador armónico vibrando en la frecuencia:
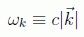
y podemos separar la dependencia temporal en la forma:
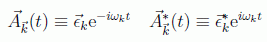
pudiendo reescribir el campo como
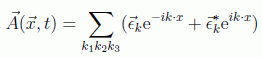
Admitiendo para los campos eléctrico y magnético la misma expansión como solución de la ecuación de d'Alembert:
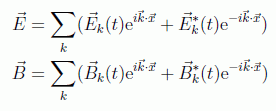
obtenemos
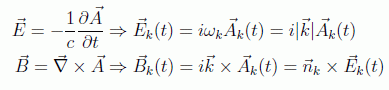
es por esto por lo que a las componentes Ak o, equivalentemente, ε, se las llama polarizaciones, ya que tienen la dirección del campo eléctrico.
Vamos a hallar la expresión de la energía para acercarnos a la cuantificación del campo. Partiendo del lagrangiano libre:
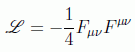
y poniéndolo en función de los campos eléctrico y magnético
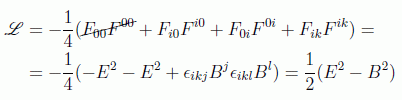
Recordando la expresión del momento conjugado:
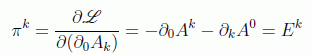
se tiene, para la densidad hamiltoniana
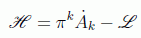
la expresión
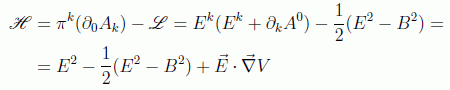
y por tanto el hamiltoniano se simplificará con las condiciones de contorno a:
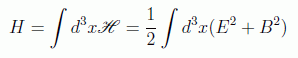
Si usamos la expresión del campo eléctrico, al calcular e integrar su cuadrado llegaremos a integrales del tipo:
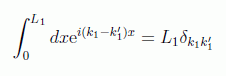
con lo que
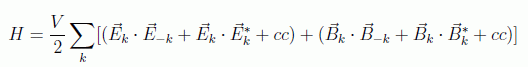
en donde a cada expresión hay que sumar el complejo conjugado (cc) y entendemos que queda claro por el contexto cuando la V se refiere al volumen, como en el caso anterior. Usando también que:
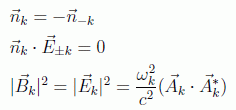
vemos que los términos transversales se cancelan:
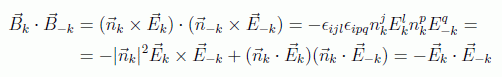
con lo que
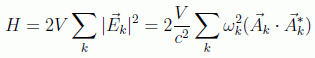
Introduciendo las coordenadas
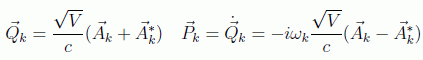
y desarrollándolas en una base ortonormal en el plano perpendicular a n:
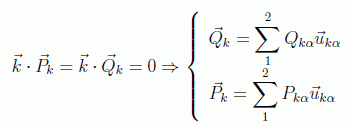
se tiene por fin para el hamiltoniano la expresión
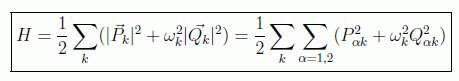
con lo que se ha demostrado que el campo electromagnético sin fuentes se puede representar como un sistema de osciladores armónicos desacoplados vibrando cada uno con frecuencia ωk y descrito por variables canónicas.
El proceso de cuantificación que iniciamos ahora, consiste en ascender el rango de las variables canónicas a operadores en el espacio de estados del sistema. Para ello definimos su actividad fundamental en analogía con los corchetes de Poisson de la mecánica clásica, por medio de la correspondencia:
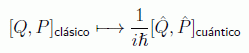
con lo que, al igual que ocurría con los corchetes fundamentales, se debe cumplir
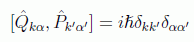
otro de los cambios al cuantificar el campo consistirá en transformar los complejos conjugados en los conjugados hermíticos (adjuntos).
Volviendo al potencial vector, su expresión en función de las variables canónicas se puede poner, ahora como operador
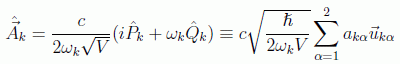
en donde se introducen los operadores
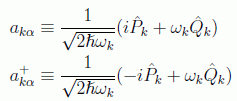
que satisfarán las relaciones de conmutación
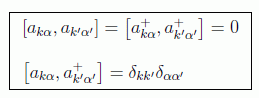
Si queremos poner el hamiltoniano en función de operadores debemos tener en cuenta que son eso, operadores, y por tanto los productos no conmutan y debemos realizar correspondencias del tipo:
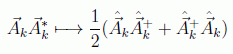
obteniendo
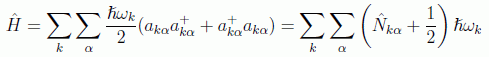
en donde el operador número es el definido en la mecánica cuántica:
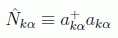
Así, el estado de cada oscilador está definido por su número de ocupación y en esta base los autovalores nos darán a su vez el valor de la energía del estado del oscilador:
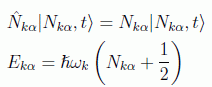
en donde se usa la representación de Schrödinger en la que son los estados los que llevan la dependencia temporal y se pueden obtener a partir del operador de creación como:
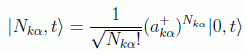
de esta forma el estado total viene definido en el espacio de Fok por cada uno de los números de ocupación de los estados de cada oscilador.
A partir del formalismo introducido vemos que hay un problema de consistencia importante. En efecto, si intentamos calcular la energía del estado fundamental nos encontramos con un término infinito:
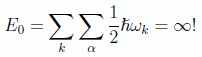
Para resolver esta dificultad del infinito en el estado de vacío utilizamos el llamado producto u orden normal, debido al físico italiano Gian Carlo Wick (denotado por una acotación de dos puntos) para los campos bosónicos, que consiste en poner siempre a la derecha los operadores de destrucción, es decir, como si conmutarán:
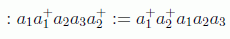
El uso de productos normales de Wick es equivalente a una renormalización del origen de energías, tomando este como el valor esperado de la energía en el vacío. En este caso el hamiltoniano y la energía de un estado genérico quedan como:
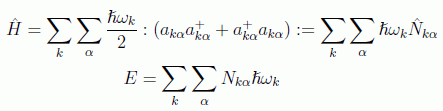
Un cálculo análogo al efectuado para el hamiltoniano podríamos hacerlo para el momento total obteniendo la expresión
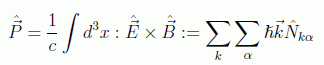
Cada estado individual se asocia con una partícula llamada fotón, γ, y definida por su energía ℏωk, momento ħk y polarización α. La partícula además es no masiva:
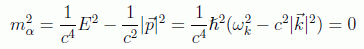
en donde se ha usado la definición de ωk y de nuevo se introducen las constantes naturales por claridad como se ha hecho a lo largo de este punto.
En el formalismo genérico esbozado al principio de este capítulo vimos cómo se favorecía naturalmente el hecho de que varias partículas ocuparan el mismo estado cuántico. En la cuantificación de la teoría de campos de estas partículas aparecían relaciones de conmutación. Sin embargo, esto no es siempre así. De hecho, esto sólo se cumple en el caso de las partículas de espín entero o bosones. El fotón estudiado es el ejemplo paradigmático.
Sin embargo, para las partículas de espín semientero prevalece el llamado principio de exclusión, enunciado por Pauli en 1925 (verlo en artículos) y según el cual nunca puede haber dos de tales partículas en el mismo estado cuántico. El principal ejemplo en este caso fue el electrón. A estas partículas se las conoce con el nombre de fermiones y el principio de Pauli, en su inicio fundamentalmente fenomenológico, perdió su condición de principio al ser integrado en el formalismo más especial de la teoría de campos y hacerlo corresponder con las distribuciones estadísticas de las partículas en la llamada conexión espín-estadística, según la cual los bosones siguen la llamada estadística de Bose-Einstein y los fermiones la de Fermi-Dirac. Este trabajo también fue elaborado por Pauli, basándose en las aportaciones del físico suizo Markus Fierz, para el congreso Solvay de 1939 que al final no se celebró debido al violento momento político imperante en Europa. Aunque más adelante intentaremos profundizar en él, vamos a apuntar alguna implicación de una teoría cuántica de campos en un espacio de Fok de fermiones.
En un trabajo fechado en 1928 (artículos), el alemán Pascual Jordan y el húngaro Eugene Paul Wigner se dieron cuenta de que para que se cumpliera la antisimetría requerida en los campos fermiónicos había que imponer relaciones de anticonmutación para los operadores creación y destrucción:
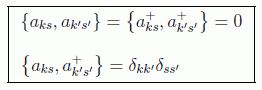
en donde ahora la s representará otro número cuántico, normalmente la tercera componente del espín.
De aquí se deduce que el cuadrado de un operador de creación o destrucción debe ser nulo:
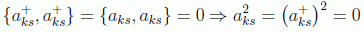
y por tanto el operador número de un estado sólo puede tener autovalores 0 o 1 ya que
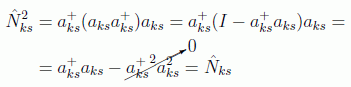
resultado que refleja a la perfección el principio de exclusión de Pauli.