
PRINCIPIO DE HAMILTON. TEORÍA DE CAMPOS

Hemos aplicado el principio extremal de Hamilton para deducir las leyes que nos engendrarán a su vez aquellas que rigen el movimiento de los sistemas en Mecánica Clásica, en donde las variables incógnita de los problemas eran las coordenadas qi(t) de las partículas puntuales. Una visión más general de los sistemas físicos nos la da la Teoría de Campos, en donde las variables dependientes a estudiar pueden ser campos en 1+3 dimensiones, un(x), como los campos electromagnético y gravitacional, densidades de carga, densidades de probabilidad, etc.
En estas teorías la variable independiente ya no es el tiempo sino el cuadrivector x del espacio-tiempo. Ya no hablaremos pues de intervalos temporales de integración sino de entornos espacio-temporales de integración. Las correspondencias principales serán:
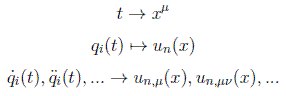
siguiendo el convenio de usar las comas para derivar parcialmente respecto de componentes del cuadrivector.
En general tendremos un conjunto de campos un(x) que pueden ser escalares, vectoriales, tensoriales, espinoriales, etc. Para simplificar, vamos a considerar un solo campo u(x), que no mermará generalidad a nuestras teorías dado el carácter aditivo de la lagrangiana.
Definimos en este caso la llamada densidad lagrangiana como la función:
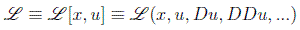
donde Du es el "vector" de componentes:
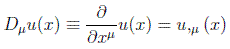
(veremos que en realidad en general este objeto tendrá otras componentes n relativas a los índices de su naturaleza y que harán que no sea un verdadero vector, pero en esta simplificación que hacemos nos valdrán este tipo de consideraciones).
Esta densidad será un objeto local real que no dependerá explícitamente de la posición x.
La lagrangiana total será entonces la integral de esta densidad extendida al dominio de x que define al sistema:
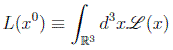
y la acción tiene una expresión análoga a la de Mecánica Clásica:
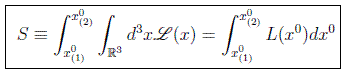
expresión no demasiado general debido al hecho de que la separación entre las componentes espaciales y temporal depende del sistema de referencia. De forma más compacta se suele poner:
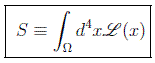
en donde Ω denota un volumen cuadridimensional.
El principio de Hamilton en este caso tendrá la forma:
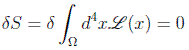
en donde la variación de los campos δu(x) se anulará en la superficie Σ de contorno de la región de integración. Una posible descripción para estas variaciones es:
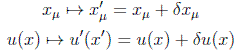
En general, para aproximaciones en primer orden, la variación general de la acción será debida por una parte a la variación general del lagrangiano y por otra a la variación del elemento de volumen debida al cambio de coordenadas. Esto no ocurre en las transformaciones de jacobiano unidad, en las que se puede afirmar que:
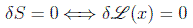
Para lagrangianos dependientes hasta primeras derivadas de los campos se tiene:
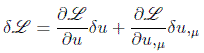
Como la variación y la derivación conmutan, se podrá integrar por partes el segundo sumando:
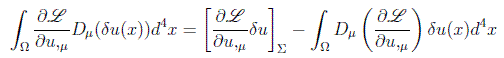
en donde el primer término se anula por anularse la variación de los campos en el contorno, quedando las ecuaciones de Euler-Lagrange en la forma:
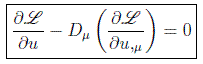
que representan un sistema de ecuaciones en derivadas parciales para cada una de las cantidades campo.
De nuevo aquí se cumple que lagrangianos distintos pueden dar lugar a las mismas ecuaciones de evolución de los campos. Esto sucede por ejemplo para los lagrangianos que difieren en una divergencia:
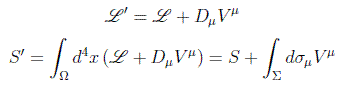
en donde se ha aplicado el teorema de Gauss Ostrogradsky. Como vemos la nueva integral de acción difiere solamente en un término de superficie, quedando:
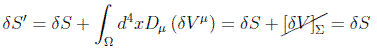
ya que las variaciones de los campos se anulan sobre las superficies límite.
Por otra parte, cuando hay más de un campo, es posible a veces encontrar lagrangianos que conducen a sistemas de ecuaciones de evolución equivalentes y que sin embargo no difieren en una divergencia. En este caso diremos que los lagrangianos son equivalentes no trivialmente.
En analogía con las ecuaciones de la Mecánica se define el momento conjugado a un campo como
Y el hamiltoniano también, asociándolo con la llamada densidad hamiltoniana:
Aquí debemos pararnos un momento. Tanto en el caso del hamiltoniano como en el anterior del lagrangiano en teoría de campos, debemos interpretar estas cantidades más que como funciones como funcionales que actuán sobre funciones- de esta forma $H$ habría que interpretarlo como $H[u,\pi]$, y cuando derivamos estas cantidades respecto a sus argumentos en realidad lo que estamos haciendo son derivadas funcionales $\delta$ del tipo:
De esta forma las ecuaciones de Hamilton en teoría de campos quedan
De la misma forma que en la teoría mecánica, en este caso si una funcional concreta $F[u,\pi]$ no depende explícitamente del tiempo se tiene como definición de los corchetes de Poisson:
Si escribimos
las derivadas funcionales son
Este resultado nos permite calcular por un lado las ecuaciones de Hamilton en función de los corchetes de Poisson:
y por otro derivar las relaciones fundamentales de conmutación, que retomaremos en teoría cuántica de campos:
Teniendo en cuenta que los campos pueden estar expresados en una representación de un grupo de simetría interno $G$ estas expresiones se deberán ampliar a
y en el caso de campos complejos