TRASLACIONES. TENSOR ENERGÍA-MOMENTO

Introducción

En este capítulo vamos a estudiar el origen del Tensor Energía-Momento que nos llevará a tratar de forma general las dos leyes de conservación relacionadas con las simetrías traslacionales, la del momento lineal y la de la energía. Este último concepto lo veremos como invariante del movimiento relacionándolo con la llamada función hamiltoniana. Probaremos también formalmente el conocido hecho de que la energía de un sistema aislado se conserva.

Tensor Energía-Momento

Forma canónica

A partir de las ecuaciones de transformación que vimos en el teorema de Noether podemos definir una traslación infinitesimal ε como el conjunto de transformaciones de punto y de campo siguientes:

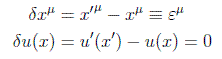
Por otra parte podemos relacionar esta variación general del campo con la variación en cada punto por medio del desarrollo infinitesimal:

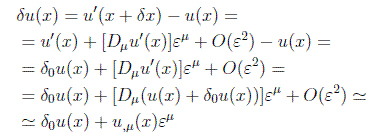
que representa el hecho de que la variación de los campos en cada punto puede ser debida a una variación intrínseca de los campos independiente de las coordenadas o consecuencia de una transformación de las mismas.

Como en este caso los campos no varían se tiene sólo la variación en cada punto que sobre estos induce la traslación:

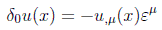
y la corriente conservada según la fórmula de la corriente del teorema de Noether será:

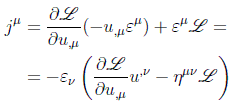
Definiendo el llamado tensor canónico de energía-momento de segundo orden como:

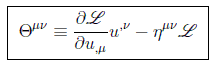
queda el teorema de Noether en su forma diferencial como:

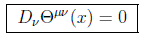
expresión que representa n leyes de conservación, μ = 0,1,2 y 3 para el caso n=4 cuadridimensional.

Con este tensor se puede calcular la energía y el momento en cualquier volumen tridimensional:

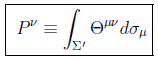
en particular para volúmenes de tiempo constante:

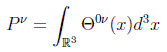
en donde Θ0ν recibe el nombre de densidad de energía-momento, siendo Pν un cuadrivector que representa la energía del sistema (cP0) y los momentos totales del sistema (P j). El resto de componentes espaciales se relacionan con las presiones del sistema.

Hay que hacer notar que la conservación de Θμν se puede deducir también a partir de las ecuaciones de Euler-Lagrange:

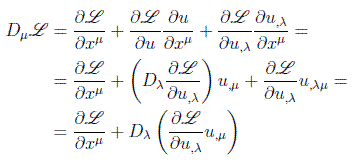
y, por tanto

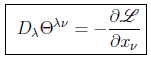
En resumen, una condición suficiente para que exista un Pν (energía-momento) conservado es que la densidad lagrangiana no dependa explícitamente de las coordenadas, en cuyo caso las corrientes conservadas son las Θμν.

Forma simétrica

En general el tensor canónico de energía-momento no es simétrico, lo que como veremos conlleva que en esta forma no se pueda usar como fuente del campo gravitatorio. No obstante, existe una técnica general de simetrización debida a Belinfante que aprovecha el hecho de que este tensor no es único, y se puede construir otro tensor equivalente al anterior que dé lugar a la misma Física.

En efecto, si al tensor canónico le añadimos una divergencia de un tensor de tercer orden θλμν(x) antisimétrico en los dos primeros índices y tal que θ0iν(x) se anule en el infinito tridimensional:

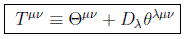
se podrá elegir convenientemente este nuevo término de forma que el nuevo tensor sea simétrico.

Veamos que en efecto este nuevo tensor representa las mismas propiedades físicas, es decir, también es conservado y nos da la misma energía y momento totales:

i) 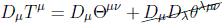, ya que el segundo término se anula por la antisimetría.

ii) 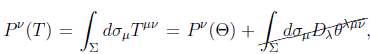, ya que el segundo término se anula por la condición de contorno impuesta.

Homogeneidad del tiempo. Energía

Sistemas libres

Cuando la lagrangiana no depende explícitamente del tiempo se puede desarrollar en serie en la forma:

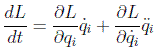
$\frac{dL}{dt}=\frac{\partial L}{\partial q_i}\dot{q}_i+\frac{\partial L}{\partial \dot{q}_i}\ddot{q}_i$

utilizando las ecuaciones de Euler-Lagrange se puede poner como

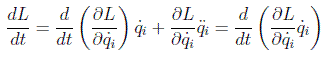
$\frac{dL}{dt}=\frac{d}{dt}\left(\frac{\partial L}{\partial \dot{q}_i}\right)\dot{q}_i+\frac{\partial L}{\partial \dot{q}_i}\ddot{q}_i=\frac{d}{dt}\left(\frac{\partial L}{\partial \dot{q}_i}\dot{q}_i\right)$

o bien

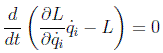
$\frac{d}{dt}\left(\frac{\partial L}{\partial \dot{q}_i}\dot{q}_i-L\right)=0$

luego, recordando la definición de momento generalizado, la cantidad:

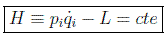
\framebox{$H\equiv p_i \dot{q}_i-L=cte$}

llamada hamiltoniano, función hamiltoniana o, a veces, energía del sistema, se conserva en la evolución.

Recordemos que en el caso de un sistema libre cuyas transformaciones no dependen del tiempo la lagrangiana era la forma cuadrática:

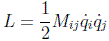
$L=\frac{1}{2}M_{ij}\dot{q}_i\dot{q}_j$

que arroja la siguiente expresión para el momento generalizado:

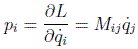
p_i=\frac{\partial L}{\partial \dot{q}_i}=M_{ij}\dot{q}_j

Por tanto, la expresión de la energía de un sistema de partículas libres será, según la definición de hamiltoniano:

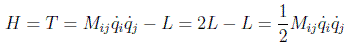
$H=T=M_{ij}\dot{q}_i\dot{q}_j-L=2L-L=\frac{1}{2}M_{ij}\dot{q}_i\dot{q}_j$

y la lagrangiana misma del sistema se conservará.

A esta hamiltoniana particular se la conoce con el nombre de energía cinética, T, por ser una cantidad conservada que sólo depende de las velocidades generalizadas y las masas del sistema.

Hay que tener en cuenta que la función H no siempre coincide con la energía física del sistema, aunque por abuso del lenguaje se le llama energía por ser una cantidad conservada. En estos casos la verdadera energía E no se conserva, y suelen coincidir con sistemas que no están verdaderamente aislados y son rehónomos (sus ligaduras dependen del tiempo). En ese caso T=T0+T1+T2 y se tienen las expresiones:

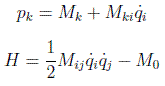
$H=\frac{1}{2}M_{ij}\dot{q}_i\dot{q}_j-M_0$

en este caso la invariante H se denomina integral de Jacobi o de Jacobi-Panlevé.

Sistemas con interacción

Como se ha dicho, en la mayoría de los casos en Mecánica los sistemas con interacción se pueden definir con una lagrangiana con la forma:

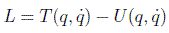
L=T(q,\dot{q})-U(q,\dot{q})

y usando la definición de hamiltoniano se obtiene:

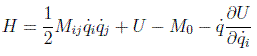
$H=\frac{1}{2}M_{ij}\dot{q}_i\dot{q}_j+U-M_0-\dot{q}\frac{\partial U}{\partial \dot{q}_i}$

expresión que, suponiendo que la función U no depende de las velocidades (caso de sistemas conservativos), y que las ecuaciones de transformación de coordenadas no dependen del tiempo (sistema esclerónomo), se reduce a la famosa:

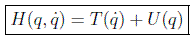
$H(q,\dot{q})=T(\dot{q})+U(q)$

que coincide con la energía del sistema. De ahí que al término U se le conozca también como energía potencial, por ser una cantidad normalmente relativa a las coordenadas de las partículas.

Homogeneidad del espacio. Momento lineal

A partir de las ecuaciones de Lagrange ya vimos que para cada coordenada cíclica o ignorable existía un momento canónico conjugado conservado:

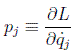
y vimos que en el caso de coordenadas generalizadas este momento tendría la forma:

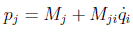
que en sistemas de referencia no dependientes del tiempo conservaría sólo el segundo término.

Para las coordenadas físicas, este momento toma la forma familiar:

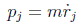
o bien, la más conocida, como vector

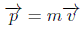
Esto constituye también una forma de definir los sistemas de referencia, dado que, respecto a un sistema de referencia arbitrario, el espacio sería no homogéneo, es decir, que aunque un cuerpo no interactúe con ningún otro, sus distintas posiciones en el espacio no serían mecánicamente equivalentes.

El hecho de buscar sistemas de referencia en donde esto no ocurra es la razón por la cual la lagrangiana no debería contener el vector posición, y vemos así que de esta premisa, homogeneidad del espacio, hemos deducido de nuevo una ley de conservación, la del momento lineal.