
TEOREMA DE NOETHER

En el contexto de la teoría de campos, e influenciada por su formación matemática en teoría de invariantes, Emmy Noether (1882-1935), propuso en 1918 el que probablemente es uno de los teoremas más bellos de la física-matemática. Viene a ser en el contexto continuo el análogo a las comentadas coordenadas cíclicas y cantidades conservadas en Mecánica.
Para el desarrollo de este teorema utilizaremos un principio que veremos en muchas ocasiones a lo largo de estos apuntes, consistente en suponer ciertas condiciones generales que deben cumplir las leyes físicas. Este principio, llamado de covariancia o invarianza de forma, afirma que las leyes de la naturaleza deben tener la misma forma en todos los sistemas de referencia equivalentes. Esta es la formulación más general del principio y en cada teoría el experimento nos dará el conjunto de sistemas de referencia que en efecto son equivalentes, que en general estarán relacionados unos con otros por las transformaciones debidas a las simetrías del sistema.
Teorema (Noether). A toda transformación continua de las coordenadas o/y los campos que deje invariante la acción en un volumen cuadridimensional le corresponde una corriente conservada jμ en la evolución que cumple Dμjμ=0.
Dem: Si consideramos el conjunto de transformaciones de punto y de campo:
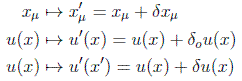
en donde ponemos subíndice o a la variación del campo en un punto particular. Inducida se tiene la variación correspondiente de la lagrangiana:
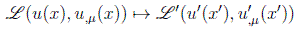
Si suponemos la covarianza del lagrangiano, éste presentará la misma forma funcional para las cantidades transformadas que para las cantidades originales, es decir:
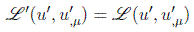
Otra de las suposiciones del teorema es la invarianza de escala, es decir, que la magnitud de la integral de acción sea invariante ante la transformación:
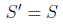
estas dos últimas condiciones reflejan las propiedades de simetría para coordenadas cíclicas ya vistas con anterioridad.
Combinando las dos últimas ecuaciones se tiene:
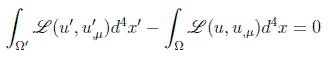
o bien, como la x' será muda:
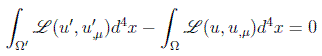
que, haciendo simbólicamente Ω'=Ω+δx , se puede poner como:
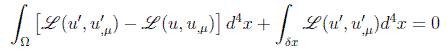
que en primer orden se convierte en:
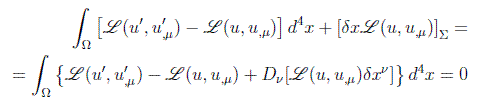
Por las ecuaciones de transformación podemos poner en primer orden:
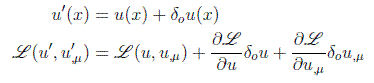
como el subíndice o representa un cambio en un punto fijo va a conmutar con la derivación espacial, y tenemos:
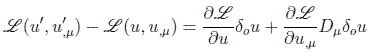
o utilizando las ecuaciones de campo de Lagrange:
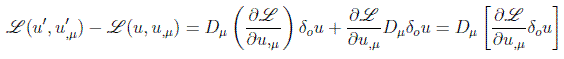
con lo que la condición de invariancia queda:
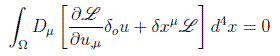
que tiene la forma de una ecuación de corriente conservada. Si definimos:
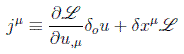
Con lo que el teorema de Noether se expresa en primer orden como:
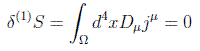
o bien aplicando el teorema de Gauss, para campos que satisfagan las ecuaciones de Euler-Lagrange, la variación general de la integral de acción en primer orden se reduce a una integral de superficie:
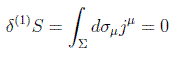
o bien directamente en su forma diferencial, la llamada ley de conservación:
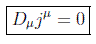
Hay que hacer notar que la corriente jμ no está unívocamente definida ya que es posible sumarle una corriente Cμ(x) conservativa trivial de forma que Dμ Cμ(x)=0.
Estas relaciones generales puramente matemáticas nos permitirán en lo que sigue obtener resultados físicos de gran interés.