PARTÍCULAS RELATIVISTAS DE ESPÍN 0

Introducción

La evolución lógica que se podía tomar para hacer una teoría cuántica relativista con el mismo modelo que se siguió para hacer la teoría de ondas de Schrodinger estaba condenada al fracaso. De hecho, no existe una ecuación de ondas análoga a la de Mecánica Cuántica que sea compatible con ésta y con la relatividad.

El mismo Schrodinger diseñó una ecuación de ondas relativista, que fue más tarde descubierta independientemente por el físico sueco Oskar Klein y el alemán Walter Gordon. Hasta su interpretación adecuada en términos de teoría cuántica de campos, fue desechada por tres razones muy justificadas:

i) No reproducía el espectro de estructura fina del átomo de hidrógeno.

ii) Se podían deducir probabilidades negativas.

iii) Permitía estados de energía negativa.

No fue hasta el año 1934, 6 años después de que Dirac propusiera su ecuación para partículas de espín 1/2, cuando W.Pauli y V. Weisskopf interpretaron correctamente la ecuación de Klein-Gordon como la que describía un campo cuántico escalar. Veremos cómo se pudieron salvar estos problemas con una nueva interpretación de la teoría en el formalismo de segunda cuantización, y de hecho esta ecuación es buena para el estudio de muchas partículas sin espín como los mesones π o piones.

Ecuación de Klein-Gordon

Para deducir esta ecuación hay que respetar, aparte del principio cuántico de que los observables aquí son operadores, la vieja fórmula para la energía relativista:

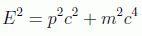
Recordemos las prescripciones cuánticas para transformar observables, según las cuales:

en donde el último símbolo corresponde al operador nabla habitual de la geometría diferencial. De aquí naturalmente se infiere:

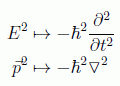
Por tanto la ecuación deseada queda como

o bien

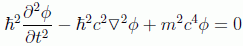
\begin{equation} \boxed{\displaystyle\frac{\partial^2 \phi}{\partial t^2}-c^2\nabla^2\phi+\frac{m^2c^4}{\hbar^2}\phi=0} \label{eq-kg1} \end{equation}

que usando unidades naturales (ħ=c=1) queda:

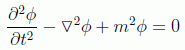
Veamos ahora su forma covariante. Si usamos la métrica habitual en teoría de partículas (1,-1,-1,-1) podemos reescribir la ecuación anterior introduciendo el operador D'Alambertiano, que constituye la generalización del operador laplaciano en un espacio de Minkowsky:

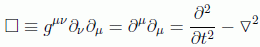
nos queda la ecuación de Klein-Gordon en su forma covariante más conocida:

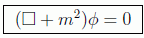
que como vemos es manifiestamente invariante relativista, siempre que φ sea una función escalar (que más adelante interpretaremos como un campo), es decir, invariante bajo una transformación Lorentz:

Límite no relativista

Si ponemos la solución de la ecuación de Klein-Gordon como

\[ \phi(x,t)=f(x,t){\rm e}^{-\frac{i}{\hbar}mc^2t} \]

y tenemos en cuenta que en el límite no relativista, la diferencia entre la energía total y la de su masa en reposo es muy pequeña, es decir

\[ T=E-mc^2\ll mc^2 \]

como $f(x,t)\sim {\rm e}^{-\frac{i}{\hbar}Tt}$ se tiene

\[ \left|i\hbar\frac{\partial f}{\partial t}\right|\simeq Tf \ll mc^2f \]

y operando un poco

\[ \begin{split} \frac{\partial \phi}{\partial t}&=\left(\frac{\partial f}{\partial t}-\frac{i}{\hbar}mc^2f\right){\rm e}^{-\frac{i}{\hbar}mc^2t}\simeq -\frac{i}{\hbar}(T+mc^2)f{\rm e}^{-\frac{i}{\hbar}mc^2t}\simeq -\frac{i}{\hbar}mc^2{\rm e}^{-\frac{i}{\hbar}mc^2t}\\ \frac{\partial^2 \phi}{\partial t^2}&=\frac{\partial}{\partial t}\left[\left(\frac{\partial f}{\partial t}-\frac{i}{\hbar}mc^2f\right){\rm e}^{-\frac{i}{\hbar}mc^2t}\right]=\left[\frac{\partial^2f}{\partial t^2}-\frac{i}{\hbar}mc^2\frac{\partial f}{\partial t}\right]{\rm e}^{-\frac{i}{\hbar}mc^2t}-\\ &-\frac{i}{\hbar}mc^2\left(\frac{\partial f}{\partial t}-\frac{i}{\hbar}mc^2f\right){\rm e}^{-\frac{i}{\hbar}mc^2t}=\\ &=\left[\frac{\partial^2f}{\partial t^2}-\frac{2i}{\hbar}mc^2\frac{\partial f}{\partial t}-\frac{m^2c^4}{\hbar^2}f\right]{\rm e}^{-\frac{i}{\hbar}mc^2t}\simeq\\ &\simeq - \left[\frac{2i}{\hbar}mc^2\frac{\partial f}{\partial t}+\frac{1}{\hbar^2}(\not{T^2}+m^2c^4)f\right]{\rm e}^{-\frac{i}{\hbar}mc^2t}\simeq\\ &\simeq - \left[\frac{2i}{\hbar}mc^2\frac{\partial f}{\partial t}+\frac{m^2c^4}{\hbar^2}f\right]{\rm e}^{-\frac{i}{\hbar}mc^2t} \end{split} \]

en donde se ha usado

\[ \frac{\partial^2 f}{\partial t}\sim\frac{\partial}{\partial t}\left(-\frac{i}{\hbar}Tf\right)\sim - \frac{T^2}{\hbar^2}f \]

y, lógicamente

\[ \nabla^2\phi=\nabla^2f{\rm e}^{-\frac{i}{\hbar}mc^2t} \]

Introduciendo estos resultados en la ecuación de Klein-Gordon \eqref{eq-kg1} obtenemos

\[ -\hbar^2\left[\frac{2i}{\hbar}mc^2\frac{\partial f}{\partial t}+\frac{m^2c^4}{\hbar^2}f\right]{\rm e}^{-\frac{i}{\hbar}mc^2t}-\hbar^2c^2\nabla^2f{\rm e}^{-\frac{i}{\hbar}mc^2t}+m^2c^4f{\rm e}^{-\frac{i}{\hbar}mc^2t}=0 \]

o lo que es lo mismo

\begin{equation} \boxed{i\hbar\frac{\partial f}{\partial t}=-\frac{\hbar^2}{2m}\nabla^2f} \label{eq_kgsch} \end{equation}

Reconocemos en esta última ecuación la ecuación de Schrödinger, para partículas sin espín. Esta sería una forma de ver que la ecuación de KG es una ecuación para partículas de espín cero, dado que el tipo de partícula no debería verse afectado por el hecho de estar en el régimen relativista o no.

Soluciones.Energías negativas

La solución en este caso es la onda plana:

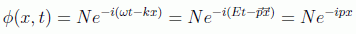
en donde se asume el producto usual entre los cuadrivectores momento y posición:

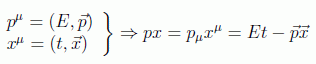
Nótese también que el cuadrado de este cuadrivector momento nos da el cuadrado de la masa, precisamente el origen de la ecuación de Klein Gordon:

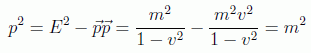
La solución apuntada es análoga a la solución de Schrödinger y no habría ningún problema de no ser porque no es la única. Esto es debido a que ahora la relación de dispersión es la relativista:

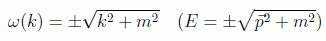
y por tanto en este caso existirán dos soluciones generales, correspondientes a valores de energía positiva y negativa:

Este hecho no tendría mucha gravedad si no hubiera transiciones entre estados. En el caso ideal de la partícula libre estos estados no deben interactuar y por tanto prodríamos quedarnos sólo con las soluciones con más sentido físico, correspondientes a energías positivas, y trabajar sin preocupación. Sin embargo, este sistema ideal no es realista y en teoría cuántica de campos hay que contemplar el hecho de que una partícula de energía E podría decaer en otra con energía -E (sin más que emitiendo un fotón de energía 2E).

Interpretar estas soluciones fue uno de los principales escollos del desarrollo de la teoría. Teniendo además en cuenta que el hamiltoniano es definido positivo, como puede verse si uno parte del lagrangiano de Klein-Gordon:

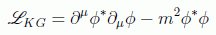
dado aquí en su forma compleja (el factor 1/2 desaparece debido a que la parte conjugada se toma como un campo distinto en las ecuaciones de Euler), del cual podemos obtener la densidad hamiltoniana a partir del momento conjugado:

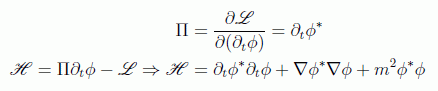
cuyo caracter positivo es manifiesto. Hay que decir que estas cantidades complejas dan lugar a dos conjuntos de ecuaciones independentes que se suelen usar para las partículas con carga. Pero como veremos el de las energías negativas no era el único problema que tenía este formalismo.

El problema de la interpretación probabilística

En el contexto no relativista, la ecuación de Schrödinger definía claramente una corriente conservada a partir de la conservación de la probabilidad. Allí llegamos a una ecuación de continuidad para la densidad de probabilidad y la corriente de probabilidad. Veremos que si intentamos hacer los mismo en el formalismo relativista nos encontraremos de nuevo con problemas de interpretación. Encontrar esta corriente es fácil teniendo en cuenta que combinando la ecuación de Klein-Gordon con su compleja conjugada se cumple:

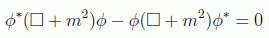
lo que implica que

Sin embargo en este caso vemos que la componente que debería corresponderse con una densidad de probabilidad no parece definida positiva:

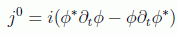
siendo la parte espacial básicamente equivalente a la que salía en el formalismo no relativista. Esto es así por el carácter de la ecuación de Klein-Gordon, que compromete una segunda derivada temporal que hace que en la ecuación de continuidad sobrevivan derivadas temporales del campo. Podemos ver más claramente el carácter no positivo de la componente temporal si aplicamos lo deducido a la solución general de la ecuación:

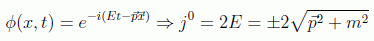
llegando a la conclusión de que en efecto podríamos obtener probabilidades negativas sin sentido físico si siguiéramos defendiendo la interpretación probabilística no relativista.

Esto sugiere que esta densidad debe ser reinterpretada como la conservación de alguna cantidad no definida positiva, como la carga eléctrica, pero no como la conservación de una probabilidad. De hecho veremos que la cantidad adecuada para una corriente de carga conservada Noether será (recuperando las constantes físicas para mayor claridad):

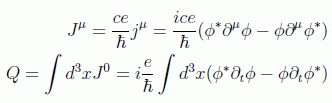
Aunque la visión clara de todo esto la tendremos en el formalismo de segunda cuantización, veamos qué forma puede tener la solución de Klein-Gordon y la carga del campo complejo bajo un punto de vista más general.

Vamos para ello a pasar a la representación en momentos, usada muy frecuentemente en teoría de partículas. Cuando hablamos de representación de momentos nos referimos a k o a p, que son iguales en unidades naturales. Muchos de los problemas de hecho se caracterizan por describir energías y momentos más que coordenadas espaciotemporales, aparte de que veremos que las expresiones ganan en claridad interpretativa.

Antes de nada, recordemos que se puede desarrollar una función en la forma de Fourier:

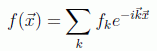
en donde se puede imaginar una caja de dimensiones Li con condiciones de contorno tales que den una cuantización para el vector de onda de la forma:

y por tanto

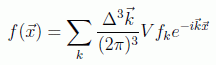
de lo que se puede suponer la forma que tendrá la suma en el continuo:

Siguiendo este mismo procedimiento se puede suponer que la integral de Fourier en el espacio de momentos correspondiente a la onda de posición tendrá la forma:

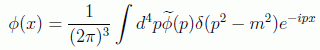
en donde el volumen V ha sido de nuevo absorbido en la función transformada y la delta de Dirac nos asegura que el integrando sólo sea distinto de cero cuando se cumpla que E2-p2=m2 o, dicho de otra forma, cuando el desarrollo satisfaga de nuevo la ecuación de Klein-Gordon:

en donde se ha hecho uso de la propiedad xδ(x)=0. A este tipo de integraciones se las denomina integraciones sobre la capa de masas. No hay que obsesionarse con las constantes que se añaden ya que cada autor sigue sus propios criterios y se pueden encontrar de varias maneras en los textos. Muchos de hecho optan por usar raices cuadradas en los denominadores para lograr simetrías con las transformadas inversas y otros siguen arrastrando las constantes físicas que no aparecen si se usan unidades naturales. Aquí intentaremos avisar de las distintas notaciones.

Aunque la expresión dada del desarrollo de Fourier en espacio de momentos es manifiestamente invariante Lorentz, es conveniente hacer actuar a la delta de Dirac para integrar sobre la componente temporal y quedarnos sólo con una integral tridimensional. Para ello hay que recordar la propiedad de la delta sobre los ceros de su argumento:

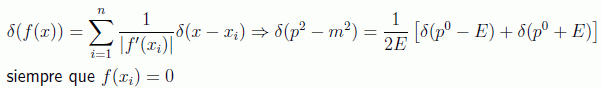
con lo que podemos separar las soluciones de energía positiva y negativa en la forma

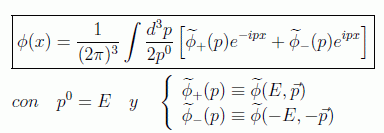
Es importante recordar que estamos tratando el caso de soluciones complejas. Para las funciones reales se debe cumplir, lógicamente:

Aunque en este caso el hecho esté más oculto, la forma integral tridimensional también es invariante Lorentz ya que el elemento de volumen ha sido deducido de un invariante Lorentz con la propiedad de la delta de Dirac ya mencionada.

Veamos la forma de la carga conservada en espacio de momentos. Para ello debemos usar la derivada temporal del campo:

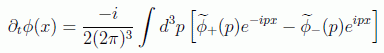
teniendo en cuenta la definición de la delta de Dirac:

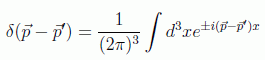
encontramos sin demasiada dificultad la expresión de la carga en el espacio de momentos (de nuevo incluyendo las constantes físicas):

en donde, aparte de confirmar el hecho de que la carga no es definida positiva, se observa que las soluciones de energía positiva y negativa contribuyen con cargas de signo opuesto, lo cual es consistente con una interpretación partícula-antipartícula.

Como ya se ha dicho, esto se entenderá mejor en la reinterpretación de los campos como operadores de creación y destrucción de partículas, de forma que las energías negativas correspondan a antipartículas asociadas con operadores de destrucción de soluciones de energía positiva.

Asimismo se ve claramente que las partículas neutras deberán estar asociadas a campos reales en donde se cumple que Q=0. Esto es así por ejemplo en el caso del campo electromagnético.

Cuantización canónica

El método que debemos seguir para cuantificar el campo de KG es análogo al ya estudiado para el campo electromagnético. Se procederá por tanto a sustituir las variables dinámicas por operadores a partir de la prescripción de Heisenberg.

El uso de conmutadores, como vimos, está restringido a las partículas de espín entero (bosones). Veremos que en el caso de los fermiones habrá que usar relaciones con anticonmutadores para obtener una descripción consistente.

A partir de esta prescripción el procedimiento de cuantificación es el de conmutador a tiempos iguales, con lo que en principio no es un formalismo invariante Lorentz:

\[ \begin{split} [\hat{\phi}(\vec{x},t),\hat{\pi}(\vec{y},t)]&=i\hslash\delta^{(3)}(\vec{x}-\vec{y})\\ [\hat{\phi}(\vec{x},t),\hat{\phi}(\vec{y},t)]&=[\hat{\pi}(\vec{x},t),\hat{\pi}(\vec{y},t)]=0 \end{split} \]

en donde podemos ver que las funciones de campo han sido ascendidas al rango de operadores denotándolos con un arco circunflejo encima. Nos olvidaremos no obstante por comodidad de esta notación y tendremos siempre en cuenta que los campos serán operadores.

La lagrangiana del sistema es en este caso:

\[ \mathscr{L}=\dot{\phi}^+\dot{\phi}-c^2\nabla\phi^+\nabla{\phi}-\frac{m^2c^4}{\hslash^2}\phi^+\phi \]

y por tanto los momentos conjugados:

\[ \pi=\frac{\partial\mathscr{L}}{\partial \dot{\phi}}=\dot{\phi}^+\qquad \pi^+=\frac{\partial\mathscr{L}}{\partial \dot{\phi}^+}=\dot{\phi} \]

La densidad hamiltoniana por su parte es:

\[ \mathscr{H}=\pi\dot{\phi}+\pi^+\dot{\phi}^+-\mathscr{L}=\pi\pi^++c^2\nabla\phi^+\nabla\phi+\frac{m^2c^4}{\hslash^2}\phi^+\phi \]

Por tanto el operador hamiltoniano será:

\[ H=\int d^3x[\pi(x)\pi(x)^++c^2\nabla\phi^+(x)\nabla\phi+(x)\frac{m^2c^4}{\hslash^2}\phi^+(x)\phi(x)] \]

y las ecuaciones de Hamilton quedan

\[ \left\{\begin{array}{l}\displaystyle i\hslash\frac{\partial}{\partial t}\phi(\vec{x},t)=[\phi(\vec{x},t),H]\\\\ \displaystyle i\hslash\frac{\partial}{\partial t}\pi(\vec{x},t)=[\pi(\vec{x},t),H]\end{array}\right. \]

con análogas expresiones para sus hermíticos.

Desarrollándolas con ayuda de las relaciones de conmutación propuestas obtenemos:

\[ \left\{\begin{array}{l}\displaystyle i\hslash\frac{\partial}{\partial t}\phi(\vec{x},t)=i\hslash \pi^+(\vec{x},t)\\\\ \displaystyle i\hslash\frac{\partial}{\partial t}\pi^+(\vec{x},t)=i\hslash\left(c^2\nabla^2\phi(\vec{x},t)-\frac{m^2c^2}{\hslash^2}\phi(\vec{x},t)\right)\end{array}\right. \]

que combinadas nos llevan de nuevo a la ecuación de Klein-Gordon, esta vez para los operadores:

\[ \frac{1}{c^2}\frac{\partial^2\phi}{\partial t^2}-\nabla^2\phi-\frac{m^2c^2}{\hslash^2}\phi=0 \]

lo que nos muestra que con las relaciones de conmutación propuestas todo cuadra, es decir, los operadores de campo también cumplen la ecuación de K-G.

Tendremos por tanto que construir un espacio de Hilbert en donde actúen estos operadores y se cumplan las ecuaciones del movimiento sobre ellos. Para ello usamos de nuevo el espacio de Fok como hicimos en el caso del campo electromagnético, es decir, la representación de números de ocupación de estados de vibración ya estudiada. Esto es lícito hacerlo en el caso libre debido al hecho de que los campos libres relativistas que representan partículas escalares satisfacen la ecuación de Klein-Gordon y por tanto se pueden expandir en desarrollos de ondas planas. (Esto no ocurre en el caso de campos con interacción, en donde se aplica la teoría perturbativa).

Recordemos que clásicamente llegamos a

\[ \phi(x)=\frac{c}{(2\pi\hslash)^3}\int\frac{d^3p}{2E_p}\left[\underbrace{\widetilde{\phi}_+(p)}_{\text{energía positiva}}{\rm e}^{-ipx/\hslash}+\underbrace{\widetilde{\phi}_-(p)}_{\text{energía negativa}}{\rm e}^{ipx/\hslash}\right] \]

Si identificamos las transformadas de Fourier de energía positiva y negativa con los operadores siguientes:

\[ \begin{split} \hat{\phi}_+(\vec{p})&=\frac{\hslash}{c}\sqrt{2E_pV}\,\hat{a}(\vec{p})\\ \hat{\phi}_-(\vec{p})&=\frac{\hslash}{c}\sqrt{2E_pV}\,\hat{b}^+(\vec{p}) \end{split} \]

estos coeficientes están elegidos de forma que los nuevos operadores serán adimensionales. Para los operadores de campo por tanto se tendrán las expresiones (olvidándonos de nuevo del gorrito de operador):

\[ \begin{split} \phi(x)&=\int\frac{d^3p}{(2\pi\hslash)^3}\frac{\hslash \sqrt{V}}{\sqrt{2E_p}}\left[a(\vec{p}){\rm e}^{-ipx/\hslash}+b^+(\vec{p}){\rm e}^{ipx/\hslash}\right]\\ \pi(x)&=\frac{\partial \phi^+}{\partial t}=i\int\frac{d^3p}{(2\pi\hslash)^3}\sqrt{ \frac{VE_p}{2}}\left[a^+(\vec{p}){\rm e}^{ipx/\hslash}-b(\vec{p}){\rm e}^{-ipx/\hslash}\right] \end{split} \]

con expresiones análogas para $\phi^+(x)$ y $\pi^+(x)$, que en principio son campos independientes a no ser que consideremos partículas neutras (operadores hermíticos) en donde $b^+=a^+$.

De estas expresiones se pueden obtener por inversión expresiones también para los operadores $a$ y $b$, que deberán cumplir las relaciones de conmutación siguientes:

\[ \begin{split} [a(\vec{p}),a(\vec{q})^+]&=(2\pi\hbar)^3\delta^{(3)}(\vec{p}-\vec{q})\frac{1}{V}\\ [b(\vec{p}),b(\vec{q})^+]&=(2\pi\hbar)^3\delta^{(3)}(\vec{p}-\vec{q})\frac{1}{V} \end{split} \]

siendo las demás conmutaciones nulas. Para el caso de volúmenes finitos los valores del momento están discretizados, y las integrales se convierten en sumas y, de acuerdo con las correspondencias ya estudiadas

\[ \begin{split} \sum_p&\longrightarrow\int \frac{d^3p}{(2\pi\hbar)^3}V\\ \delta_{pp^\prime}&\longrightarrow \frac{(2\pi\hbar)^3}{V}\delta^{(3)}(\vec{p}-\vec{p}^\prime) \end{split} \]

se obtienen

El hamiltoniano en términos de estos nuevos operadores tiene por tanto la forma

\[ \begin{split} \hat{H}&=\int\frac{d^3p}{(2\pi\hbar)^3}VE_{\vec{p}}[a^+(\vec{p})a(\vec{p})+b(\vec{p})b^+(\vec{p})]=\\ &=\int\frac{d^3p}{(2\pi\hbar)^3}VE_{\vec{p}}\left[a^+(\vec{p})a(\vec{p})+b^+(\vec{p})b(\vec{p})+\frac{(2\pi\hbar)^3}{V}\delta^{(3)}(\vec{p}-\vec{p}^\prime)\right] \end{split} \]

El último término de nuevo carece de sentido físico ya que asociaría una energía infinita al vacío, como se puede ver en la expresión discreta:

\[ \hat{H}=\sum_{\vec{p}}E_{\vec{p}}[a_{\vec{p}}^+a_{\vec{p}}+b_{\vec{p}}^+b_{\vec{p}}+1] \]

Estos términos de nuevo desaparecen si prescribimos el orden normal ya definido para nuestros operadores:

\[ \hat{H}=\int d^3x:\left[\pi\pi^++c^2\nabla\phi^+\nabla\phi+\frac{m^2c^4}{\hbar^2}\phi^+\phi\right]: \]

quedando por ejemplo para el caso discreto

\[ \hat{H}=\sum_{\vec{p}}E_{\vec{p}}[a_{\vec{p}}^+a_{\vec{p}}+b_{\vec{p}}^+b_{\vec{p}}] \]

que se puede comparar con el del campo electromagnético

\[ \hat{H}=\sum_k\sum_\alpha\hbar\omega_ka_{\vec{k}\alpha}^+a_{\vec{k}\alpha} \]

viendo las dos claras diferencias que tiene el campo de KG estudiado, por un lado la ausencia de un índice de polarización (la helicidad del fotón es consecuencia de ser una partícula de espín 1) y la presencia de los operadores $b$ consecuencia de considerar un campo con carga (el operador $A$ era hermítico).\\

De la misma forma podríamos calcular el operador momento

\[ \hat{\vec{P}}(t)=-\int d^3x[\pi\hat{\nabla}\phi+\hat{\nabla}\phi\pi^+] \]

que nos daría las expresiones

\[ \begin{split} \hat{\vec{P}}&=\int\frac{d^3p}{(2\pi\hbar)^3}V\vec{p}(a^+(\vec{p})a(\vec{p})+b(\vec{p})b^+(\vec{p}))\\ \hat{\vec{P}}&=\sum_{\vec{p}}\vec{p}(a_{\vec{p}}^+a_{\vec{p}}+b_{\vec{p}}b_{\vec{p}}^+) \end{split} \]

no siendo necesario en este caso el orden normal debido a la cancelación de $\vec{p}$ y $-\vec{p}$ en la suma. Se puede por tanto definir el cuadrivector de la teoría como

Espacio de estados

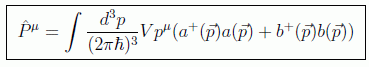
De forma análoga a como hicimos en el caso del campo electromagnético, vamos a construir el espacio de Hilbert sobre el que actúan los operadores campo, cuya representación más inmediata es la de números de ocupación (espacio de Fok).

Para las dos clases de osciladores existentes se definen dos operadores número hermíticos de la forma:

\[ \hat{N}_{\vec{p}}^{(a)}\equiv a^+(\vec{p})a(\vec{p})\qquad \hat{N}_{\vec{p}}^{(b)}\equiv b^+(\vec{p})b(\vec{p}) \]

De esta forma la energía de cada grupo de osciladores con momento $\vec{p}$ se podrá desglosar como

\[ \hat{H}_{\vec{p}}^{(a)}\equiv E_{\vec{p}}\hat{N}_{\vec{p}}^{(a)}\qquad \hat{H}_{\vec{p}}^{(b)}\equiv E_{\vec{p}}\hat{N}_{\vec{p}}^{(b)} \]

correspondiendo a las contribuciones de los dos tipos de particulas.

El hecho de que estos operadores conmuten nos permite afirmar que se pueden definir autoestados comunes, siendo sus autovalores los números de ocupación:

\[ \begin{array}{l} \hat{N}_{\vec{p}}^{(a)}\left\vert N_{\vec{p}}\right\rangle^{(a)}=N_{\vec{p}}\left\vert N_{\vec{p}}\right \rangle^{(a)}\\ \hat{N}_{\vec{p}}^{(b)}\left\vert N_{\vec{p}}\right\rangle^{(b)}=N_{\vec{p}}^\prime\left\vert N_{\vec{p}}\right\rangle^{(b)} \end{array} \]

Asimismo se pueden interpretar los operadores $a^+$ y $a$ y $b^+$ y $b$ como los de creación y destrucción de partículas y antipartículas respectivamente, siendo las antipartículas las correspondientes a las soluciones de energía negativa (que no obstante contribuyen en este formalismo con una cantidad positiva de energía).

\[ \left. \begin{array}{l} [\hat{N}_{\vec{p}},a_{\vec{p}}^+]=a_{\vec{p}}^+\\ \text{}[\hat{N}_{\vec{p}},a_{\vec{p}}]=-a_{\vec{p}} \end{array} \right\} \Rightarrow\left\{ \begin{array}{l} \hat{N}_{\vec{p}}a_{\vec{p}}^+\left\vert N_{\vec{p}}\right\rangle=(N_{\vec{p}}+1)\left\vert N_{\vec{p}}\right\rangle\\ \text{}\hat{N}_{\vec{p}}a_{\vec{p}}\left\vert N_{\vec{p}}\right\rangle=(N_{\vec{p}}-1)\left\vert N_{\vec{p}}\right\rangle \end{array} \right. \]

siendo el estado fundamental aquel en el que

\[ \hat{N}_{\vec{p}}\left\vert 0\right\rangle=0 \]

Los autoestados por tanto se pueden definir como

\[ \left\vert N_{\vec{p}}\right\rangle^{(a)}=\frac{1}{\sqrt{(N_{\vec{p}})!}}a_{p}^+a_{p}^+\cdots a_{p}^+\left\vert 0\right\rangle^{(a)} \]

Concluimos por tanto que los operadores $a^+(\vec{p})$ y $b^+(\vec{p})$ crean partículas y antipartículas respectivamente, y los $a(\vec{p})$ y $b(\vec{p})$ las destruyen. Dividiendo también el campo de KG se puede poner

\[ \hat{\phi}(x)=\hat{\phi}_+(x)+\hat{\phi}_-(x) \]

con lo que

\[ \left.\begin{array}{l} \displaystyle \hat{\phi}_+(x)=\int\frac{d^3p}{(2\pi\hbar)^3}\frac{\hbar\sqrt{V}}{\sqrt{2E_{\vec{p}}}}a(\vec{p}){\rm e}^{-i/\hbar px}\\ \displaystyle \hat{\phi}_-(x)=\int\frac{d^3p}{(2\pi\hbar)^3}\frac{\hbar\sqrt{V}}{\sqrt{2E_{\vec{p}}}}b^+(\vec{p}){\rm e}^{i/\hbar px} \end{array}\right\}\Rightarrow\left\{\begin{array}{l} \displaystyle \hat{\phi}_-^+(x)=\int\frac{d^3p}{(2\pi\hbar)^3}\frac{\hbar\sqrt{V}}{\sqrt{2E_{\vec{p}}}}a^+(\vec{p}){\rm e}^{i/\hbar px}\\ \displaystyle \hat{\phi}_+^+(x)=\int\frac{d^3p}{(2\pi\hbar)^3}\frac{\hbar\sqrt{V}}{\sqrt{2E_{\vec{p}}}}b(\vec{p}){\rm e}^{-i/\hbar px} \end{array}\right. \]

campos definidos en la representación de Heisenberg (los estados son constantes en el tiempo) y cuya interpretación es clara: $\hat{\phi}_+(x)$ destruye una partícula en el punto $x$ y $\hat{\phi}_-(x)$ crea una antipartícula en el punto $x$, y los adjuntos hacen lo contrario (los subíndices $+$ y $-$ solo se ponen para indicar que son soluciones de energía positiva y negativa respectivamente).

Si utilizamos la representación espacial en lugar de la de números de ocupación un estado de muchas partículas localizadas en $\vec{x}_1,\dots,\vec{x}_n$ será:

\[ \left\vert\vec{x}_1,\dots,\vec{x}_n;t\right\rangle\equiv \phi_-^+(\vec{x}_1,t)\cdots\phi_-^+(\vec{x}_n,t)\left\vert 0 \right\rangle \]

y en el espacio de Fok un estado general con $N_1$ partículas de momento $\vec{p}_1$, $N_2$ partículas de momento $\vec{p}_2$, etcétera, será

\[ \left\vert N_1,N_2,\dots\right\rangle=\frac{(a_1^+)^{N_1}(a_2^+)^{N_2}\cdots}{(N_1!N_2!\cdots)^{1/2}}\left\vert 0\right\rangle \]

Y la función de onda correspondiente al estado anterior en la representación de coordenadas se puede poner como

\[ \phi_{N_1,N_2,\dots}(x_1,\dots,x_n)=\left\langle\vec{x}_1,\cdots,\vec{x}_n;t\vert N_1,N_2,\cdots\right\rangle \]

con $n=N_1+N_2+\cdots$. Se tratará de una función simétrica respecto al intercambio de partículas, y si pusiéramos el ejemplo de las antipartículas sería igual, lo que indica que las partículas de espín cero cumplen la estadística de Bose-Einstein.