
ECUACIONES DE HAMILTON

Después de abordar la teoría de Lagrange sobre los sistemas mecánicos y el principio de Hamilton del que se deducen las ecuaciones del movimiento en el espacio de configuración o de coordenadas, vamos a ver ahora una formulación ligeramente diferente para conseguir las ecuaciones del movimiento de un sistema físico descritas en el espacio de fases, es decir, de coordenadas y velocidades.
En el fondo se trata de formulaciones equivalentes, pero el formalismo de Hamilton nos dará potentes herramientas que podremos exportar más allá de la Mecánica Clásica, como veremos en los temas dedicados a la Mecánica Cuántica, por ejemplo.
Las ecuaciones de Euler-Lagrange son n ecuaciones de 2º orden cuyas soluciones, las n funciones qi(t), vienen determinadas por 2n valores iniciales correspondientes a las coordenadas y velocidades iniciales. El enfoque de Hamilton será ahora ahora conseguir 2n ecuaciones diferenciales de primer orden con esas mismas 2n condiciones iniciales. Ahora las soluciones, además de las qi(t), serán otras n variables independientes, las cantidades de movimiento generalizadas definidas por:

Esto por tanto definirá un nuevo marco de descripción en el llamado
espacio de fases  frente a la anterior descripción
frente a la anterior descripción
 . El paso de una descripción a otra viene definido por
la llamada transformación de Legendre que explicamos a
continuación.
. El paso de una descripción a otra viene definido por
la llamada transformación de Legendre que explicamos a
continuación.
Vamos a trabajar por claridad con solo un par de variables en las funciones. Se trata de, dada una función en unas variables, pasar a otra transformada de forma que las primeras derivadas sean la inversa una de la otra, es decir:
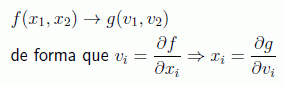
Esto se consigue por ejemplo si ensayamos para la función g la forma:
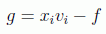
de este modo

Así, en el caso de que las funciones dependan de otras variables que no formen parte de la transformación:
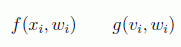
se tendrá
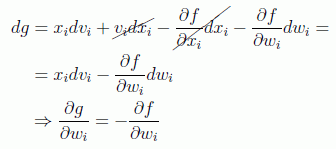
Trasladando esto a nuestro problema de Mecánica tenemos que buscar una nueva función:

para ello se define la hamiltoniana con la forma:
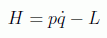
y así
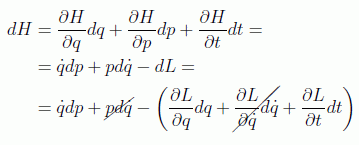
lo cual nos lleva a
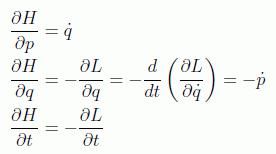
en donde se han aplicado las ecuaciones de Euler-Lagrange en la segunda identidad.
Hemos llegado pues a las ecuaciones que buscábamos. A partir de una nueva función definida en el espacio de fases, la hamiltoniana del sistema:
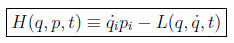
llegamos a un sistema de 2n ecuaciones del movimiento de primer orden equivalentes a las de Euler-Lagrange, las ecuaciones canónicas de Hamilton:
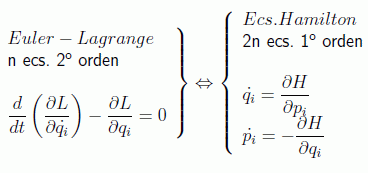
Para resolver problemas en Mecánica es crucial elegir las coordenadas generalizadas más simétricas según el problema de que se trate de modo que todas o la mayor parte de ellas sean cíclicas. De este modo, de cada coordenada cíclica saldrá una ecuación de integración inmediata:
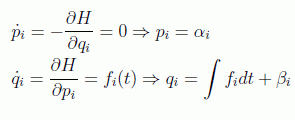
que como vemos será de inmediata integración si la hamiltoniana no depende del tiempo. Cada coordenada cíclica dependerá de dos constantes de integración (αi,βi). Si todas son cíclicas el problema por supuesto depende de las 2n condiciones.
Es por ello crucial encontrar una transformación de coordenadas que nos lleve a una descripción máximamente simétrica, y en el formalismo de Hamilton habrá que incluir también los momentos, por medio de las siguientes transformaciones:
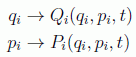
Pero además, en este formalismo tan solo nos interesarán las nuevas coordenadas que están relacionadas por las ecuaciones de Hamilton, llamadas coordenadas canónicas, y por tanto las transformaciones canónicas exigirán que exista una nueva función:
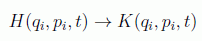
que actúe como hamiltoniana del nuevo marco, es decir, que se cumpla:
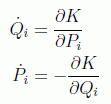
Por supuesto para que se cumplan las ecuaciones del movimiento es necesario que se siga cumpliendo el principio de Hamilton tanto en las nuevas coordenadas como en las antiguas, es decir:
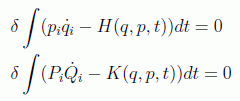
o, dicho de otro modo, la diferencia entre los dos integrandos debe ser una diferencial exacta:

A la función F se la conoce como función generatriz de la transformación porque nos hará de puente entre las antiguas variables y las nuevas.
Como las ecuaciones de transformación son $2n$ relaciones entre las $4n$ variables, en realidad sólo $2n$ variables son independientes, por lo que se puede elegir la forma funcional de la función generatriz de cuatro maneras distintas según las circunstancias del problema:

En el primer caso se tiene:

y sustituyéndolo en la diferencia de hamiltonianas y teniendo en cuenta que todas las 2n variables elegidas qi y Qi son independientes se llega a:
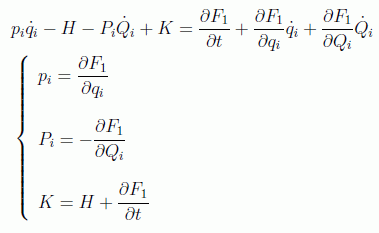
Para los siguientes casos hay que seguir utilizando F1 y por medio de transformaciones de Legendre se llega a los siguientes conjuntos de ecuaciones:
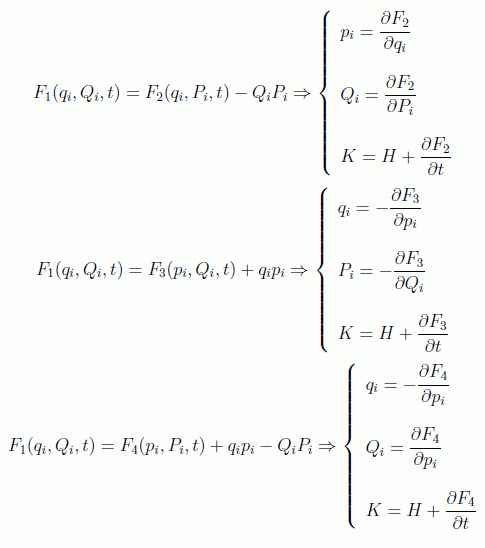
Por ejemplo, si ensayamos una función de la forma
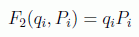
las ecuaciones de transformación serán:
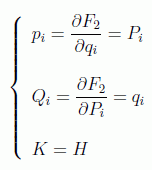
en este caso F2 genera la transformación identidad.
Vamos a estudiar uno de los más importantes de los llamados invariantes canónicos, es decir, aquellas expresiones que conservan la forma bajo transformaciones canónicas. Si consideramos las dos funciones:

se puede definir el llamado corchete de Poisson de las funciones u y v con respecto a las variables q y p como:
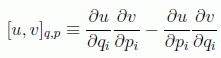
expresión bilineal antisimétrica de estructura simpléctica.
Lógicamente si u y v se eligen como las propias variables canónicas se tiene:
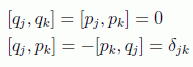
a estos últimos corchetes se los denomina fundamentales y no se pone subíndice porque valen para todo sistema de variables canónicas. Son por tanto invariantes canónicos.
Manipulando ligeramente los corchetes de partida haciendo la variación sobre otras variables canónicas se tiene:
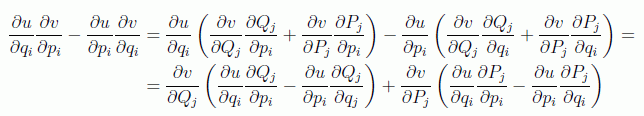
o, de forma más compacta:
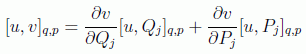
Pero por otra parte se tiene, aplicando la misma identidad anterior, que
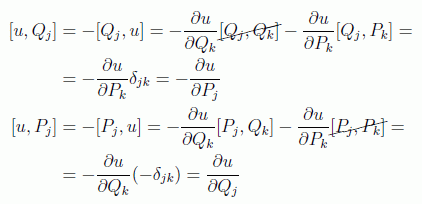
en donde se omiten los subíndices por ser expresiones canónicamente invariantes. Pero usándolas vemos que el mismo corchete de Poisson es un invariante canónico, ya que
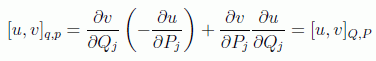
y por tanto a partir de ahora se pueden omitir los índices en todos los corchetes de Poisson.
Veremos más adelante que existe una formulación de la Mecánica Clásica, paralela a la de Hamilton, formulada con corchetes de Poisson. Con esta formulación es particularmente sencillo el paso a la Mecánica Cuántica, mediante el llamado principio de correspondencia y una adecuada definición del conmutador de operadores cuánticos.
Si hacemos u=H en las fórmulas obtenidas en el apartado anterior se pueden poner las ecuaciones de Hamilton como
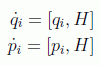
que constituyen un caso particular de la ecuación de movimiento generalizada para una función arbitraria f(q,p,t) ya que, con las ecuaciones de Hamilton se tiene
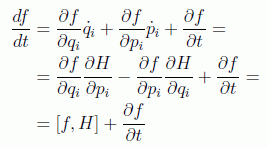
De hecho se puede deducir que si f es constante del movimiento df/dt=0 se tiene:

con lo que se tiene que las funciones constantes del movimiento que no dependan explícitamente del tiempo deben tener un valor de corchete de Poisson nulo con la hamiltoniana:
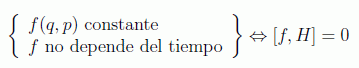
Este hecho nos proporciona un método para buscar constantes del movimiento.
Una de las propiedades más conocidas del corchete de Poisson es que cumple la identidad de Jacobi:

Con esta identidad se pueden demostrar el llamado teorema de Poisson, que afirma que el corchete de dos constantes es también una constante del movimiento:
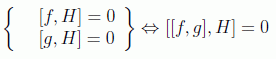
Se trata de considerar las transformaciones del tipo

La función generatriz por tanto deberá diferir muy poco de la estudiada en el caso de la transformación identidad, es decir

en donde ε es un factor infinitesimal y llamaremos a G función generatriz de la transformación infinitesimal.
Aplicando las ecuaciones de transformación

lo que implica

Pero además, si nos quedamos sólo con infinitésimos de primer orden podemos poner que:
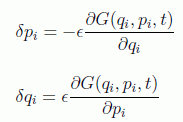
Particularmente, si consideramos la hamiltoniana como función generatriz de la transformación infinitesimal y el parámetro un cambio infinitesimal del tiempo se tiene:

y se puede describir el movimiento del sistema como una transformación infinitesimal generada por la hamiltoniana. De hecho, dado que el movimiento de un sistema mecánico es una evolución continua de transformaciones infinitesimales, la hamiltoniana es la generatriz del movimiento del sistema con el tiempo.
Por otra parte, para cualquier función de las coordenadas y los momentos, u(qi,pi), se tiene:
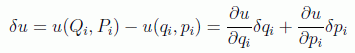
que, aplicando las ecuaciones canónicas de transformación infinitesimal vistas, se tiene:
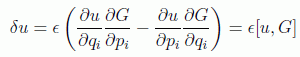
y en particular para el cambio en la hamiltoniana se tendría
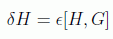
lo que indica que las constantes del movimiento (cuyo corchete con la hamiltoniana se anula) serán también las generatrices de las transformaciones canónicas infinitesimales (que dejarán invariante la hamiltoniana).
En particular las coordenadas cíclicas, cuyas transformaciones podemos poner, por ejemplo en el caso de una q_j como:
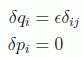
definirán como se sabe una constante del movimiento, su momento canónico conjugado, que representará la función generatriz de la transformación infinitesimal:
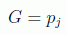
La teoría de Hamilton-Jacobi se basa en encontrar una transformación canónica de forma que las nuevas variables nos den precisamente las 2n constantes del movimiento, es decir, que sean los 2n valores iniciales (q0,p0) en t=0. Esto lo conseguimos exigiendo que la hamiltoniana transformada K se anule:
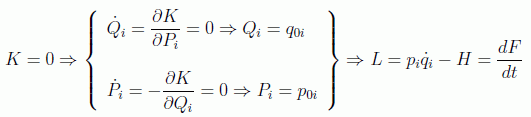
que en todos los posibles casos de dependencia estudiados para la función generatriz F conduce a la expresión:
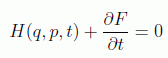
Se acostumbra a designar por S a la solución de esta ecuación, llegando a la forma más conocida de la ecuación de Hamilton-Jacobi:

Nótese que S, la llamada función principal de Hamilton, es una primitiva de la lagrangiana:
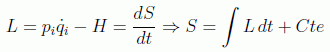
pero este hecho carece de validez práctica, ya que para calcular esa integral debemos conocer la dependencia de las coordenadas con el tiempo, es decir, haber resuelto primero el problema mecánico que es precisamente el que intentamos resolver.
La ecuación de Hamilton-Jacobi es una ecuación diferencial de primer orden con n+1 variables, las coordenadas y el tiempo, y por lo tanto dependerá de n+1 constantes de integración. Sin embargo, como la propia S no aparece en la ecuación, existe la posibilidad de sumar cualquier constante a la función S y seguirá siendo solución:
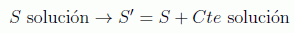
y por tanto una de las constantes, que aparezca en forma aditiva, será irrelevante, y la función principal de Hamilton será de la forma:
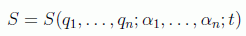
en donde podemos suponer que se trata de una función generatriz de tipo F2 y tomar las constantes de integración como las nuevas cantidades de movimiento:
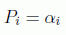
y las ecuaciones de transformación nos darán la solución del problema mecánico:
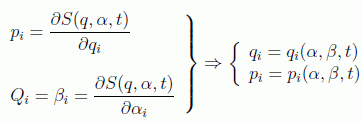
Nótese que la primera de las ecuaciones en el instante inicial nos relaciona las constantes de integración α con los valores iniciales q0i y p0i.