
LA ECUACIÓN DE SCHRÖDINGER

En 1926, el físico austríaco Erwin Schrödinger derivó una ecuación de ondas desde el principio variacional de Hamilton inspirándose en la analogía existente entre la Mecánica y la Óptica. Esta ecuación, cuya formulación se puede ver en el artículo An Undulatory Theory of the Mechanics of Atoms and Molecules de la revista Physical Review, explicaba mucha de la fenomenología cuántica que se conocía en aquel momento.
Aunque estaba claro que esta ecuación describía la evolución temporal del estado cuántico de un sistema físico no relativista, fue pocos días después de su publicación cuando el físico alemán Max Born desarrolló la interpretación probabilista del objeto principal de la ecuación, la función de onda, que sigue vigente hoy en día ya que entró a formar parte de la llamada interpretación de Copenhague de la Mecánica Cuántica, con la que Schrodinger nunca estuvo del todo de acuerdo. Sus ambiciones al abordar la tarea eran encontrar, en analogía con la Óptica, el límite en el cual se pudieran describir de forma determinista las trayectorias de las partículas. Llegó a proponer una interpretación de la función de onda como densidad de carga que no fructificó. En este sentido Schrödinger fue, al igual que Einstein, profeta y hereje de la teoría cuántica.
El desarrollo que haremos aquí no es el histórico. Partiremos de principios de simetría apoyados en el teorema de Wigner, físico húngaro artífice entre otros de la llamada interpretación ortodoxa de la Mecánica Cuántica, para llegar a una formulación general que devenirá la original de Schrödinger cuando nos ocupemos de la representación en el llamado espacio de posiciones.
Como se ha dicho en estos apuntes, las leyes físicas deben ser invariantes bajo ciertas simetrías, representadas por las transformaciones de los objetos matemáticos que definen estas leyes. En particular en Mecánica Cuántica cabe preguntarse por las transformaciones de los estados y de los observables:

En el caso cuántico estas transformaciones deben cumplir lo que constituye la esencia del llamado teorema de Wigner, es decir, que los observables transformados deben poseer los mismos conjuntos posibles de valores que los antiguos (autovalores) y que las transformaciones de los estados nos deben dar las mismas probabilidades, deben estar siempre dadas por operadores unitarios que conservan los productos escalares:
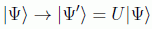
en realidad el teorema permite también los operadores antiunitarios, pero estos sólo se usarán para determinados tipos de simetrías.
Por tanto la expresión de los observables transformados está dada por:
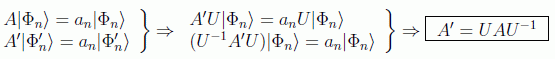
Si enfocamos nuestra atención a las transformaciones infinitesimales:
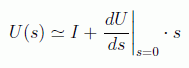
la unitariedad demanda:
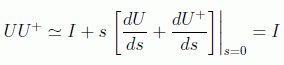
que implica que la derivada será de tipo imaginario puro:
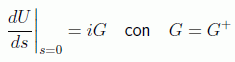
luego suponiendo U(0)=I esos operadores unitarios deben tener la forma
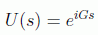
siendo G los generadores de las transformaciones asociadas a los parámetros s. En el caso general multiparamétrico tendríamos las relaciones
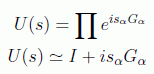
Estos generadores obedecerán, como vimos en el capítulo de teoría de grupos, una serie de relaciones de conmutación. Si consideramos dos transformaciones y sus inversas:
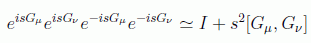
y teniendo en cuenta que cualquier composición de transformaciones debe equivaler, salvo fase, a otra transformación del grupo, se tiene, observando que:
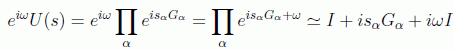
que el conmutador de dos generadores será una combinación lineal de generadores y el operador identidad:
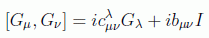
en donde el último término se puede hacer cero haciendo ω=0 y las constantes c serán fruto de la idiosincrasia de las transformaciones a considerar.
En el caso que nos ocupa la dinámica de una partícula libre, suponiendo velocidades no relativistas, debería ser invariante bajo las transformaciones del grupo de Galileo, cuyos 10 parámetros definen, como se sabe, los siguientes operadores unitarios asociados a cada simetría:

en donde se introducen signos menos por convención. Para hallar las ecuaciones del movimiento nos preguntaremos por la evolución temporal:
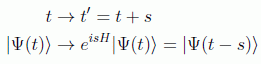
es decir, haciendo s=t:
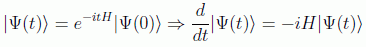
que constituirá la ecuación del movimiento de la función de onda. Por razones históricas es conveniente redefinir el operador H por H/ħ (eventualmente se usará un sistema de unidades en el que ħ=1), quedando la ecuación del movimiento como:

en donde el generador H es el hamiltoniano del sistema. Destacar que muchos textos introducen esta ecuación como uno de los postulados de la Mecánica Cuántica.
Siguiendo con nuestra discusión, vamos a sacar la ecuación de evolución para el operador estado. Primero observemos que la evolución de la función de onda desde un instante inicial t0 está dada por:

Este operador evolución deberá satisfacer por tanto también la ecuación del movimiento:
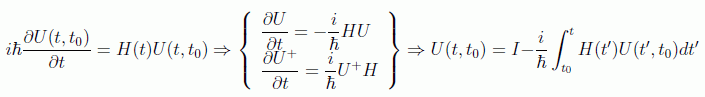
en donde lógicamente se supone que U(t0)=I.
Si H es independiente del tiempo (sistemas conservativos) el operador evolución tendrá la forma:
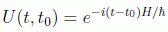
de lo contrario no tendrá una forma concreta y dependerá del caso a estudiar. Vamos a ver qué sucede con los operadores estado. Supongamos que no perdemos generalidad al considerar un operador representando un estado puro:
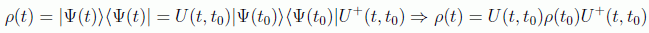
Derivando respecto al tiempo y usando la ecuación del movimiento para U se tiene:
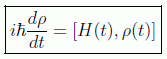
Si prestamos nuestra atención a la evolución temporal de los valores medios de los observables:

vemos que hasta ahora hemos supuesto que la dependencia temporal explícita la lleva el estado, esta es la llamada imagen de Schrödinger, pero observando que:
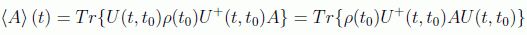
podemos suponer que la dependencia temporal la llevan los operadores observables, definiendo:
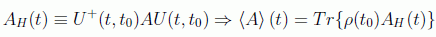
lo que constituye la llamada imagen de Heisenberg, en donde son las variables dinámicas las que evolucionan.
En el caso de un estado puro, las medias tienen la forma, en la imagen de Schrödinger y en la de Heisenberg respectivamente:
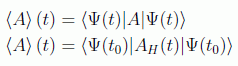
Podemos deducir las ecuaciones de evolución de los observables en la imagen de Heisenberg, suponiendo que el hamiltoniano también se desarrolla en esa imagen:
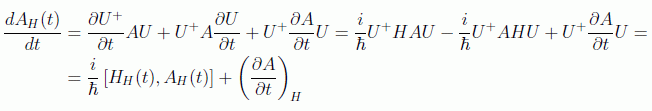
En esta imagen el operador estado sólo dará cuenta de los datos iniciales de la preparación del experimento. La evolución de la media será por tanto:
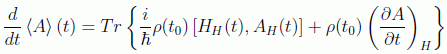
mientras que en la imagen de Schrödinger tendremos la fórmula similar:

En el caso de un estado puro la fórmula general de evolución de un valor esperado está dada por:
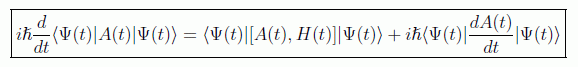
lo que indica que para un sistema arbitrario la evolución del valor esperado de un observable es debida en parte a la evolución del vector estado y en parte a la dependencia explícita en el tiempo del observable.
De aquí también se puede apreciar que una constante del movimiento es un observable que no depende explícitamente del tiempo y que conmuta con H:

de lo que se deduce que para sistemas conservativos el hamiltoniano será una constante del movimiento.
Asumiendo que el espacio es continuo y que las tres componentes del vector posición x=(x1,x2,x3) de la partícula son cinemáticamente independientes, podemos suponer que los operadores que las representan son mutuamente conmutativos, lo que equivale a decir que poseen un conjunto común de autovectores, de forma que:
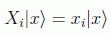
La representación de posición o representación en el espacio de posiciones o de coordenadas o de configuración del espacio de Hilbert que estudiamos será aquella en donde los vectores estén desarrollados en la base ortonormal de la posición, es decir:
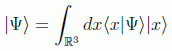
con las relaciones de ortonormalidad y cierre habituales para los espacios continuos:

Los coeficientes en la expansión definen funciones de variable continua que a menudo se suelen identificar con la función de onda propiamente dicha, por ser esta la definición original:
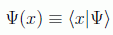
Los operadores actuarán por simplicidad indistintamente en el espacio de Hilbert o en el espacio funcional. Para ver la forma que tiene el operador momento en esta representación debemos recordar su papel de generador de traslaciones:
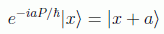
de forma que, para traslaciones infinitesimales
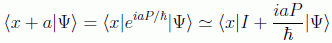
que en el espacio funcional toma la forma
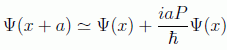
comparándolo con el desarrollo de Taylor en análisis tenemos que
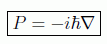
cuyas componentes en coordenadas cartesianas tienen la forma simple

apariencia que no es tan sencilla en cualquier otro tipo de coordenadas generalizadas.
La ecuación de onda de Schrödinger para una partícula sometida a un potencial escalar V(x) vendrá dada por la expresión del hamiltoniano no relativista, que suponemos que es, en la representación de posición:
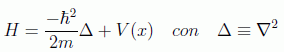
y por tanto tenemos
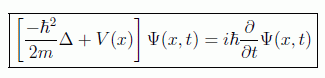
Una de las observaciones que hay que hacer acerca de la ecuación de Schrödinger es que, como no podía ser de otra manera, conserva la norma del vector de estado:
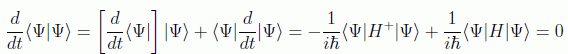
que es una forma equivalente de expresar la unitariedad de la evolución o la hermiticidad del hamiltoniano.
Ahora vamos a ir más allá y vamos a ver cómo evoluciona la probabilidad, para cerciorarnos de que no encontremos fuentes ni sumideros de la misma en nuestro dominio de definición. Para ello vamos a definir la llamada densidad de probabilidad como
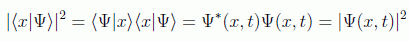
que nos daría, como vimos en el postulado III, si la integramos sobre un volumen dado, la probabilidad de que la partícula se encuentre en ese volumen en el instante t. Veamos pues cómo evoluciona en dos instantes de tiempo:
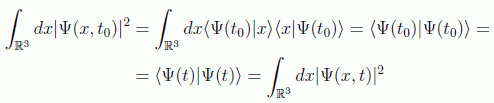
en donde se ha usado la conservación de la norma. Por otra parte podemos escribir, para un volumen arbitrario Ω, usando la ecuación de Schrödinger:

en donde se ha usado el teorema de la divergencia de Gauss, siendo n el vector unitario normal hacia el exterior de Ω, y la llamada densidad de corriente de probabilidad:
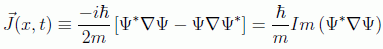
y, como la región Ω es arbitraria, llegamos a la ecuación de continuidad:
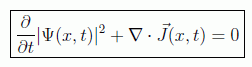
formalmente idéntica a la ecuación de un fluido sin fuentes ni sumideros, es decir, la probabilidad se propaga como un fluido.
Lógicamente, si elegimos el volumen de integración de forma que coincida con todo el espacio tridimensional, debido a las condiciones de acotación de la norma la función de onda se anulará en la superficie del infinito, el segundo término de la ecuación de continuidad se anulará y recuperaremos la conservación de la norma propiamente dicha. En la mayoría de los casos esto de hecho sucederá aún si restringimos nuestro volumen al dominio del problema.
Para hallar soluciones de la ecuación se suele ensayar el método de separación de variables, que funciona siempre que la energía potencial no dependa del tiempo, y consiste en suponer para la función de onda la forma factorizada:
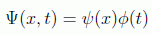
llegando a la conclusión de que esta función debe ser de la forma:
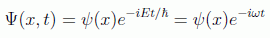
en donde E es la energía total de la partícula, ω la frecuencia angular de la onda asociada y la parte espacial debe satisfacer la llamada ecuación de Schrödinger independiente del tiempo:

En este caso la ecuación se reduce, teniendo en cuenta la expresión clásica de la energía cinética (E=p2/2m), llegando a la ecuación:
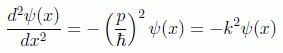
en donde k es el llamado número de onda angular, inverso de la longitud de onda, que se deduce de la relación de de Broglie p=ħk, y las soluciones serán de la forma:
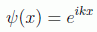
con lo que una solución particular de la ecuación de Schrödinger será la onda plana monocromática:
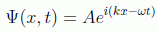
sin olvidar que la frecuencia depende de la longitud de onda por la relación de dispersión de la partícula libre:
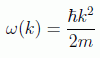
Esta solución describe una onda viajera ya que, por ejemplo, los nodos de su parte real se encuentran en los puntos x=(n+1/2)π/k+ωt/k, que se van desplazando con el tiempo.
La densidad de probabilidad en este caso no nos aporta información ya que las amplitudes de las ondas son las mismas en todas la regiones espaciales:

lo que indica que la partícula se encontrará con la misma probabilidad en cualquier punto del espacio. Podemos calcular el valor medio del momento de la partícula, que estará dado por:
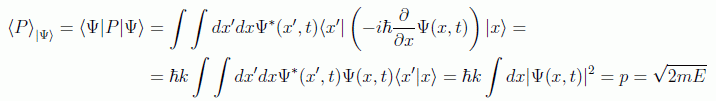
en donde hemos hecho actuar la delta de Dirac y la condición de normalización.
No obstante, la solución de partícula libre a la ecuación de onda no es normalizable en todo el espacio, no pertenece a las funciones de cuadrado integrable y no se ajustaría a los postulados de la Mecánica Cuántica. Este es un viejo caballo de batalla en la Física de los sistemas ideales, no sólo cuánticos, que a veces dan lugar a inconsistencias matemáticas. Para empezar, tampoco tiene mucho sentido el considerar todo el espacio euclídeo como el laboratorio de nuestra partícula. Además, un sentido mucho más realista del problema es considerarlo como un proceso límite de un verdadero fenómeno físico descrito por un paquete de onda, es decir un grupo de ondas viajeras. En efecto, es muy aventurado asegurar que la partícula se encuentra en un estado con un momento lineal perfectamente definido, se acerca más a la realidad suponer una distribución de momentos. De este modo la densidad de probabilidad correspondiente será más aproximada a la descripción del movimiento de la partícula libre. No obstante, las matemáticas necesarias para describir el grupo de ondas analíticamente son muy complicadas y las dejaremos para un capítulo posterior.
En cualquier caso, para hacernos una idea más aproximada de lo que estamos hablando, podemos hacer una descripción aproximada del comportamiento de un paquete de ondas suponiendo una distribución en números de onda (es decir, energías, momentos) debida tan solo a dos componentes ondulatorias:
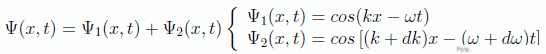
usando la identidad trigonométrica:
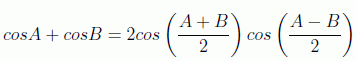
encontramos la expresión (para dk<<2k y $dω<<2k$):
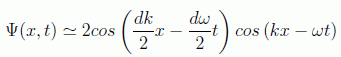

que podemos representar, para los instantes t=0 y t=20, en cualquier programa de representación online como el Wolfram Alpha o el propio Google, con los valores correspondientes a ħ=m=k=1, obteniendo algo como en la figura, en donde se ve claramente el viaje del grupo y cómo la densidad de probabilidad sería más aproximada a nuestra experiencia.
Vemos que el segundo factor de la onda es como la inicial pero modulada por el primer factor, de forma que las oscilaciones de Ψ caen dentro de una envolvente cuya amplitud varía periódicamente. Las ondas se interfieren y se refuerzan alternativamente.
La velocidad de las ondas individuales se puede evaluar considerando el segundo factor en los nodos de la función:

vemos que esta velocidad de la onda no es igual a la velocidad de la partícula que representa. Esto es así porque la velocidad que debe tener correspondencia con la partícula es la llamada velocidad de grupo, que se evalúa considerando los nodos del primer factor de la onda:
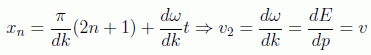
Estas consideraciones sobre el movimiento de la partícula se pueden continuar calculando los valores promedios de los observables y recuperando, al menos formalmente, las leyes de la Mecánica Clásica, lo que constituye el contenido del llamado teorema de Ehrenfest.
Como hemos visto, el estudio de la partícula libre no arroja ninguna condición para la energía. Vamos a empezar a ver ahora los llamados estados ligados, que como veremos darán lugar naturalmente al hecho típico de la Mecánica Cuántica de que la energía suele estar discretizada o cuantizada en sólo unos estados permitidos determinados por el problema.
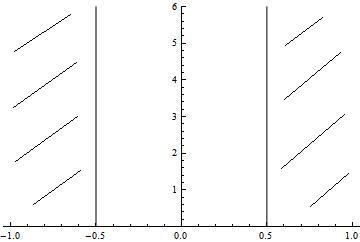
El más sencillo de estos problemas es el del pozo cuadrado, en donde tenemos una zona de ancho a en donde la partícula no se ve sometida a potencial alguno y a ambos lados de esta zona se tiene un potencial constante de altura V0.
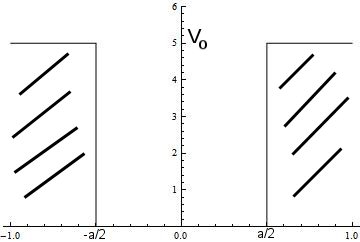
En la figura vemos un esquema y el potencial concreto tiene la forma:
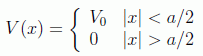
Lógicamente se trata de una situación idealizada, pero puede servir para estudiar cualitativamente sistemas físicos sencillos como un electrón de conducción en un bloque de metal. Por supuesto supondremos los casos en que la energía de la partícula sea menor que la altura del pozo:
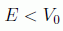
para los que, según la Mecánica Clásica, la partícula sólo podría estar en la región |x|<a/2 (dentro del pozo).
La solución general de la ecuación de Schrödinger independiente del tiempo dentro del pozo es la que hayamos para la partícula libre, esta vez con las constantes de integración añadidas:

que representa ondas que viajan en sentido positivo y negativo de x respectivamente. No obstante, la simetría del problema sugiere la igualdad en valor absoluto de las constantes de integración, lo que lleva a considerar mejor las siguientes soluciones generales:
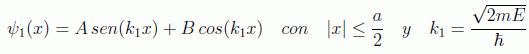
suma de dos ondas estacionarias en donde se conocerá el momento de la partícula pero no su sentido de movimiento.
Para el caso hipotético en que la partícula se encuentre fuera del pozo, como su energía es menor que la potencial, la ecuación a resolver será:
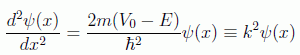
que tendrá las soluciones, en la regiones que llamaremos 0 (x<a/2) y 1 (x>a/2), que a continuación se detallan:
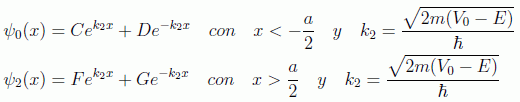
Estas ondas estacionarias no tienen nodos, pero deben superponerse con las ondas estacionarias del interior del pozo que sí tienen nodos. El hecho de que la función de onda debe ser normalizable anula las ramas divergentes de las soluciones, con lo que D=F=0, con lo que las soluciones en esas zonas del pozo quedarían:
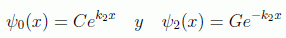
Nos resta obtener por tanto las cuatro ecuaciones más para las constantes restantes, y eso se realiza demandando que ψ y dψ/dx sean continuas en las dos fronteras. Los cálculos nos llevan a dos ecuaciones trascendentes que se deben satisfacer independientemente, es decir, hay dos conjuntos de soluciones, las correspondientes a función de onda par:

y las correspondientes a la función de onda impar:
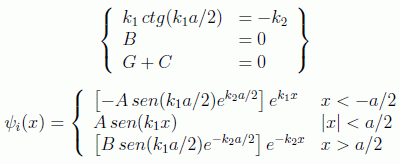
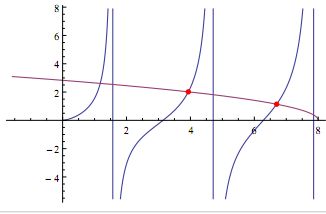
Las constantes se ajustan por las condiciones de normalización. Un ejemplo de la forma de estas funciones se puede ver en la figura:
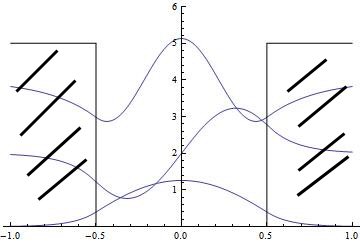
El hecho de que la paridad de las soluciones esté definida es consecuencia de que la ecuación de Schrödinger de partida es invariante bajo el cambio x---< -x y lo podíamos haber supuesto de inicio llegando a la misma forma de solución.
Los niveles de energía y por tanto la escala concreta de las autofunciones hay que calcularla resolviendo numéricamente las dos ecuaciones trascendentes halladas:
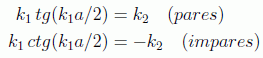
lo cual se puede hacer en cada caso por varios métodos, y en donde se encuentran como dijimos al inicio las energías discretizadas correspondientes a los puntos de corte de las gráficas como en la figura.
De esta forma encontramos que sólo existen un número restringido de valores permitidos de la energía para E<V0 que corresponderán a los estados ligados de la partícula, estando permitido cualquier valor para E>V0, es decir, ahí formarán un continuo como en el caso de la partícula libre. Tendremos al menos un estado ligado dependiendo de la altura del pozo, correspondiente a una función par.
Una de las consecuencias más notables de estos primeros cálculos cuánticos es que hay regiones no accesibles por la Mecánica Clásica en donde existe cierta probabilidad de encontrar a la partícula. Esto es así porque en las paredes del pozo finito la función de onda no se hace nula, sino que existe cierto rango de penetración. Esta distancia de penetración, para el caso de un electrón en un metal, por ejemplo, es del orden de las dimensiones atómicas y en la mayoría de los casos muy pequeña respecto al ancho del pozo. Esto sugiere tratar con otro ejemplo límite en el cual el pozo de potencial tenga un valor inaccesible o infinito (en el caso del metal sería un superficie del metal cuya distribución de carga creara un potencial neto insalvable para el electrón).
Por tanto el siguiente paso natural es considerar el llamado potencial cuadrado infinito o pozo de paredes infinitas, que a menudo se conoce como el estudio de la partícula en una caja.
En este caso todos los estados están ligados y por tanto la energía está cuantizada en todo su dominio. La forma analítica vendría dada por:
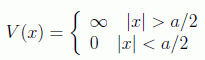
como se vio las soluciones dentro del pozo tienen la forma estacionaria:
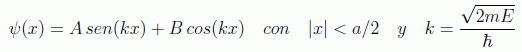
En este caso, a diferencia del caso del pozo finito, no puede haber regiones de penetración en la barrera en donde la función de onda sea no nula. Esto es así por las características del límite:
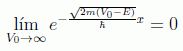
y la función de onda deberá ser
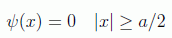
y como consecuencia la onda estacionaria en este caso tendrá nodos en las paredes de la caja y además no podremos exigir continuidad a la derivada en esos puntos.
Aplicando estas condiciones en los dos puntos frontera obtenemos:
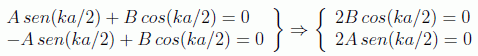
que son precisamente las condiciones de cuantificación que, al no poder satisfacerse simultáneamente, definen de nuevo dos clases de autofunciones, pares e impares:
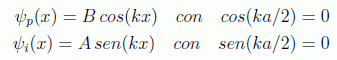
Las ecuaciones trascendentes para el número de onda (y por tanto la energía) en esta ocasión son triviales y conducen a las soluciones:
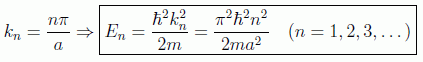
en donde se ha ignorado la solución n=0 porque correspondería a una función de onda idénticamente nula y, por tanto, a la inexistencia de la partícula. De aquí se deduce otra de las características de la Mecánica Cuántica, que la partícula no puede tener energía total cero, es decir, la energía de punto cero o energía más baja que puede tener la partícula será:
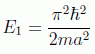
este resultado es consecuencia del principio de incertidumbre que veremos más adelante.
Las condiciones de normalización para las funciones de onda arrojarán valores concretos para las constantes:
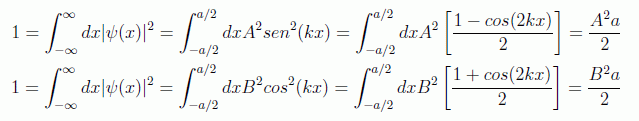
con lo que la expresión final de estas funciones será
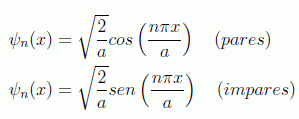
que se pueden ver en la figura para a=1.

El primer caso realista de potencial lo constituye el oscilador armónico. Este potencial es de enorme importancia ya que se puede obtener su solución analíticamente y es modelo para multitud de sistemas físicos, desde el estudio de las vibraciones de átomos en moléculas diatómicas hasta las vibraciones de las ondas electromagnéticas en teoría cuántica de campos.
Para vibraciones pequeñas escogiendo adecuadamente los ejes el potencial a estudiar tiene la forma parabólica:
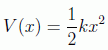
donde k es la llamada constante de recuperación, ya que una partícula que se mueva sobre su influencia experimentará una fuerza restauradora lineal F=-kx (ley de Hooke).
La ecuación de Schrödinger independiente del tiempo tendrá la forma
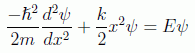
teniendo en cuenta la expresión de la frecuencia clásica de oscilación:
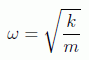
la ecuación resulta
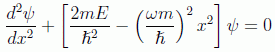
Por comodidad se introducen los parámetros:
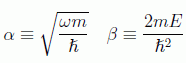
con lo que la ecuación a resolver será
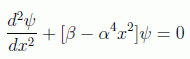
Rescalando la variable x adecuadamente se puede poner:
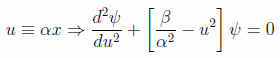
que para valores muy grandes de u toma la forma:
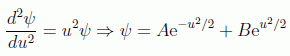
pero como la función de onda debe converger en el infinito se tiene:
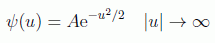
lo cual sugiere que se busquen soluciones generales de la forma:
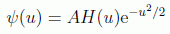
de forma que H(u) no explote en el infinito como una exponencial. Sustituyendo en la ecuación se tiene, para la función H(u):
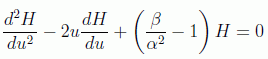
ecuación diferencial que, al contrario que la original, se puede resolver por la técnica de series de potencias. Identificando coeficientes y obteniendo relaciones de recurrencia entre ellos, se obtiene la solución en términos de dos series (una par y otra impar):
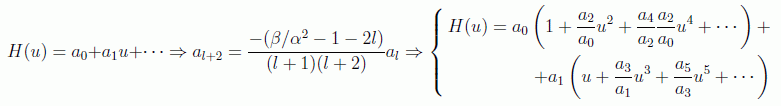
De nuevo imponemos convergencia. Es claro que para u grandes los términos de las potencias bajas en u no son considerables, pero las razones de los términos de potencias altas de las series son análogos a los de la exponencial cuadrática:

como esta función no converge, hay que cortar la serie de potencias en algún valor de l=n, definido por
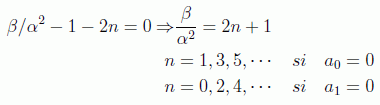
Esta solución resultante ya no define una serie infinita sino unos polinomios llamados polinomios de Hermite:
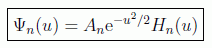

en donde la regla de cuantificación obtenida ahora se puede poner como
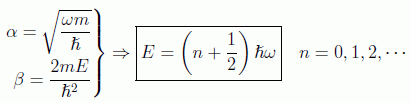
Las funciones ψ2n(x) son pares y las ψ2n+1(x) son impares. La constante de normalización toma la forma:
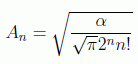
Teniendo en cuenta que los primeros polinomios de Hermite son de la forma:
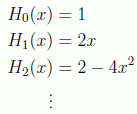
podemos ver en la figura la representación gráfica de los primeros autoestados:
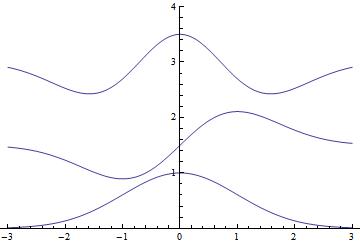
Los niveles de energía son análogos a los deducidos por Planck y los físicos de la teoría cuántica antigua, salvo que aquí la energía de punto cero es ħ ω/2 (como veremos que exige el principio de incertidumbre).
Este método comienza por definir los operadores:
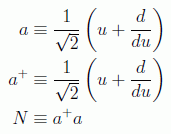
en donde el último es formalmente hermítico, como se puede ver sacando su expresión en términos de las variables dinámicas y el hamiltoniano:
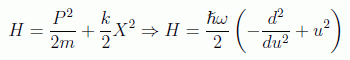
y por tanto

de donde también se deducen las expresiones:

Vamos a ver que en efecto los autovalores del operador N son los enteros no negativos, y es por esto por lo que se le conoce como operador número. Para empezar tengamos en cuenta los conmutadores:
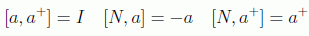
y supongamos que |n> es el autovector normalizado del operador N con autovalor n: N|n>=n|n>, entonces:

es decir, a|n> y a+|n> son autovectores de N con autovalores n-1 y n+1 respectivamente, dicho de otra forma, son proporcionales a los autovectores |n-1> y |n+1>. La constante de proporcionalidad se calcula mediante la norma:
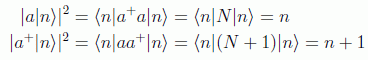
con esto ya queda claro que n >= 0, es decir, N es definido positivo, aparte de deducirse las fórmulas:
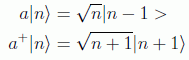
en donde en el primer caso n no podrá ser cero. A los operadores a y a+ se los denomina operadores destrucción y creación respectivamente por estar relacionados con la desaparición y aparición de cuantos. Nótese que además a|0>=0.
Todavía no hemos demostrado que los n son enteros. Es muy fácil, por reducción al absurdo, imaginemos que existe un autovalor semientero q:
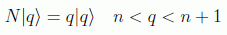
es fácil darse cuenta de que se puede construir una cadena de autovectores ap|q> de N con autovalores q-p:

y por tanto an|q> es autovector de N con autovalor (q-n)>0, y si aplicamos a podemos construir el autovalor no nulo:
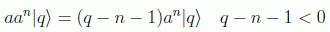
lo cual es absurdo ya que según vimos no podían existir esos autovalores negativos. Luego n debe ser un entero no negativo.
En resumen, hemos probado que los autoestados del hamiltoniano son de la forma
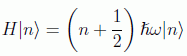
que pueden ser generados a partir del fundamental como
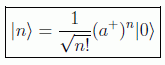
Si queremos recuperar la solución analítica, podemos hacerlo mediante:
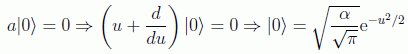
y aplicando ahora el operador de creación se encuentra
