
TEORÍA DE GRUPOS

Observar las simetrías que posee la Naturaleza es el objetivo principal de la Física Fundamental, ya que de ahí también podremos deducir las leyes que la gobiernan. El concepto de grupo está íntimamente ligado al de simetría y es por eso que antes debemos abordar este capítulo, fundamentalmente matemático, e intentar hacernos una visión general del funcionamiento de estos objetos.
Hay que decir primero que el origen de la teoría de grupos está en el intento de los matemáticos por resolver ecuaciones algebraicas de grados arbitrarios por medio de radicales, es decir, dando fórmulas a aplicar para sacar las raíces de la ecuación. Primero los árabes en la edad media y después los algebristas italianos en en el siglo XVI sólo llegaron a obtener expresiones radicales para órdenes 2, 3 y 4.
No fue hasta los albores del siglo XIX cuando se resolvió el llamado problema de la quinta insoluble gracias al teorema del matemático noruego Abel en 1824, basado también en el trabajo del matemático italiano Ruffini, en el que demostraron que no se podían encontrar expresiones radicales en ecuaciones de grado mayor o igual a cinco (lo cual, lógicamente no negaba la existencia de esas soluciones, sino la forma de obtenerlas).
Hoy se sabe, no obstante, que todas estas aportaciones son parte de una teoría más general, debida al matemático francés Galois, el verdadero creador de la teoría de grupos. En su teoría no sólo se demuestra la imposibilidad de ecuaciones de grado mayor o igual que cinco, sino que además se da la razón por la cual las ecuaciones de grado menor que cinco se pudieron resolver por radicales, cosa que la teoría de Abel no hacía.
La trágica historia de Galois, muerto a los 20 años, es muy conocida entre los físicos teóricos y no le voy a dedicar demasiado espacio. Sólo dar un par de pinceladas y decir que resulta muy interesante por la personalidad del sujeto y los determinantes acontecimientos en los que se vio envuelto. Nacido en París en 1811, a pesar de sus indudables actitudes intelectuales, Galois fue rechazado en su examen de ingreso en la Escuela Politécnica y se matriculó en la Escuela Normal. Alentado no obstante por uno de sus profesores, dio vida a una de las teorías más influyentes de las matemáticas e intentó que muchos de los matemáticos de su época le escucharan mandándoles sus trabajos. No tuvo éxito. Debido según unos a sus convicciones republicanas (llegó a estar encarcelado seis meses) y según otros a un desamor, fue retado a duelo el 29 de Mayo de 1832 y murió el día siguiente a consecuencia de una herida en el abdomen. Su trabajo sólo fue reconocido mucho después de su muerte.
La utilización del aparato de la teoría de grupos en la Mecánica Cuántica fue propuesta en la década de los años 30 del siglo pasado, casi simultáneamente, por Wigner y Weyl.
Se llama grupo a cualquier conjunto G de transformaciones de simetría que cumple:
1) Existe una ley de composición interna, normalmente llamada
multiplicación o suma:
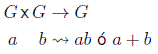
2) La ley es asociativa:

3) Existe un elemento neutro e:
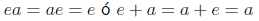
a este elemento se le denomina 1 en la multiplicación o 0 en la suma.
4) Todo elemento a posee inverso a-1 (o -a en la
suma, en cuyo caso se suele llamar simétrico):
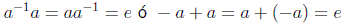
A veces los postulados 3) y 4) se sustituyen por otros más débiles pero equivalentes en donde sólo aparece la multiplicación(suma) por la izquierda.
Cuando un subconjunto H de G conserva las propiedades de grupo con la misma operación se denomina subgrupo de G. En todo grupo hay dos subgrupos, llamados impropios, que son él mismo y la identidad.
Si todos los elementos del grupo conmutan el grupo se denomina conmutativo o abeliano. Una forma de medir el grado de conmutatividad de un grupo es mediante la operación de conjugación:

lógicamente, si el grupo es conmutativo todos sus elementos coinciden con sus conjugados y sólo existirá una clase de equivalencia de conjugación.
Un subgrupo H de G se denomina normal o invariante o autoconjugado si sus conjugados con cualquier elemento de G permanecen en H (todo subgrupo de un grupo abeliano es normal). Si un grupo sólo tiene los subgrupos normales triviales se denomina simple. A los grupos triviales (la identidad y el mismo grupo) a veces se les denomina subgrupos impropios. Por tanto, un grupo será simple si no posee subgrupos normales propios. Diremos que un grupo es semisimple si no posee subgrupos normales abelianos propios.
El grupo se llamará finito si tiene un número finito de elementos. A este número se le llama orden del grupo y se denota como |G|. En caso contrario hablaremos de un grupo infinito.
Un ejemplo de grupo finito sería el grupo de permutaciones de 3 elementos, S3, perteneciente a los llamados grupos simétricos por coincidir con el conjunto de aplicaciones biyectivas que se pueden establecer, en este caso entre los tres elementos. Lógicamente, el orden aquí sería |S3|=3!=6.
El grupo infinito más común es el conjunto de matrices invertibles de orden n sobre un cuerpo K, que normalmente es el de los reales o los complejos, tomando como operación interna la multiplicación de matrices. Hay que tener en cuenta que el orden aquí no es el orden del grupo sino el de las matrices que lo representan. Este grupo se conoce con el nombre de grupo general lineal de orden n:
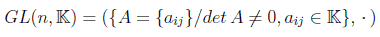
Un grupo H es homomorfo a otro G si existe una correspondencia entre ambos que conserve la operación de grupo. Con esta condición, dos elementos del grupo inicial pueden ir al mismo del final pero la identidad se transformará en identidad en el otro grupo. Si este mapeo es biyectivo se denominará isomorfismo de grupos. Si el isomorfismo se realiza sobre el mismo grupo se llamará automorfismo.
Para los grupos finitos se puede definir un subconjunto, denominado sistema de generadores, S, consistente en un conjunto de elementos del grupo tales que sus productos (o los productos de sus inversos) generan el grupo. El conjunto generado se denota de la siguiente forma:

Vamos a verlo con el conjunto de permutaciones de 3 elementos, que se sabe que tiene orden 6:
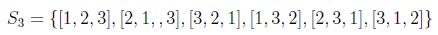
Los elementos del grupo se suelen denotar mejor como
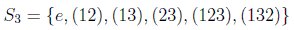
indicando las permutaciones de 1 o de 2 elementos. En general aquí vemos que es un grupo no abeliano, ya que:
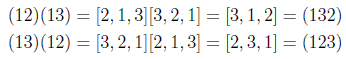
en donde se ha usado la composición de permutaciones de la siguiente forma:
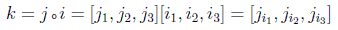
Se puede comprobar que las trasposiciones del primer elemento con el segundo y con el tercero generan todo el grupo:
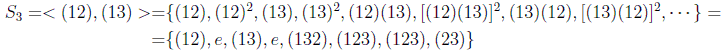
En general el grupo Sn se genera con n-1 trasposiciones:

Los grupos de permutaciones se pueden dividir en las permutaciones impares y las pares. En este caso, el grupo alternado de 3 elementos, A3, que es como se denominarían las permutaciones pares, cuyo orden es la mitad que el principal, sería de la forma:
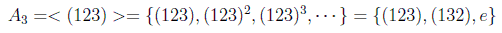
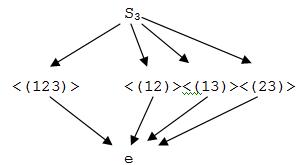
Una forma sencilla de representar las generaciones de un grupo finito es mediante los llamados grafos de Cayley:
Como dato, sin entrar en detalles, decir que Galois asoció a cada polinomio un grupo de permutaciones de sus raíces. Abel había demostrado que el A5 era un grupo simple y como consecuencia S5 era no resoluble, es decir, no existía una serie de subgrupos invariantes contenidos consecuentemente (todo grupo abeliano es, obviamente, resoluble). Galois de hecho demostró que el primer grupo simple no abeliano tenía orden 60 (es decir, que el A5 de Abel era el primero no resoluble).
Para los grupos infinitos, podemos utilizar la estrategia de etiquetar sus elementos ga, o bien, g(a), entendiendo a como un conjunto de parámetros que viven en un espacio topológico. De esta forma, podremos hacer una correspondencia entre ese espacio y los elementos del grupo, y muchas veces identificar ambos. Se asume que estos parámetros son esenciales, es decir, caracterizan completamente a cada elemento del grupo.
Dentro de los grupos infinitos, hay un conjunto importante, los denominados grupos continuos, que nos garantizan que si:
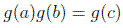
entonces c debe ser una función continua en los parámetros a y b.
A su vez, dentro de los grupos continuos hay un conjunto de grupos denominados grupos de Lie, en honor del matemático noruego Sophus Lie que los estudió a finales del siglo XIX, en donde se debe cumplir además que esa función de los parámetros sea analítica.
Como generalización de los grupos finitos, un grupo continuo con un número de parámetros finito a veces se denomina grupo continuo finito y el número de parámetros esenciales el orden del grupo.
No hay que confundir el orden del grupo de Lie con la dimensión del
espacio donde viven sus parámetros. Por ejemplo, el grupo
GL(n,R) actúa sobre un espacio de dimensión n pero su
orden es n2 (el número de elementos de sus matrices), por tanto
se puede decir que vive en el espacio 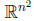 . En el caso
de que el cuerpo fuera el de los complejos, el orden del grupo sería
2n2. Este orden (a veces se le llama también dimensión, por abuso
del lenguaje) se puede restringir si nos fijamos en los subgrupos.
Por ejemplo, en el subgrupo de matrices unitarias:
. En el caso
de que el cuerpo fuera el de los complejos, el orden del grupo sería
2n2. Este orden (a veces se le llama también dimensión, por abuso
del lenguaje) se puede restringir si nos fijamos en los subgrupos.
Por ejemplo, en el subgrupo de matrices unitarias:

se tienen las n2 condiciones:
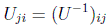
lo que reduce el número de parámetros esenciales de nuevo a n2. Y si el grupo es especial, es decir, las matrices tienen determinante unidad:
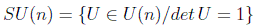
por la condición añadida se reduce el orden del grupo a n2-1.
El grupo además será compacto si el dominio de variación de sus parámetros es cerrado y acotado. En este sentido, por ejemplo, el grupo de rotaciones es un grupo compacto (sus parámetros varían en el conjunto [0,2π]) mientras que el grupo de traslaciones no es compacto.
Consideremos el grupo de matrices ortogonales, normalmente definido sobre el cuerpo real como:
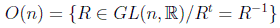
este grupo, cuyo orden es n(n-1)/2, nos da las siguientes condiciones cuando se impone RtR=1:

utilizando el convenio de Einstein de suma sobre índices
repetidos. Esto representa un conjunto de n2 ecuaciones
algebraicas, lo que implica que el dominio de los parámetros es
cerrado. Además, es claro que  (de hecho,
(de hecho,
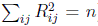 ) luego el conjunto es acotado. Por tanto, los
grupos ortogonales son compactos.
) luego el conjunto es acotado. Por tanto, los
grupos ortogonales son compactos.
Sophus Lie mostró que las principales características de un grupo se pueden deducir de aquellos elementos que difieren infinitesimalmente de la identidad. De este modo a cada grupo de Lie podemos asociarle un álgebra de Lie, que captura totalmente la estructura local del grupo.
Para empezar decir que siempre podemos reparametrizar el grupo de forma que sus parámetros sean normales, es decir, que el origen de la variedad coincida con la identidad del grupo, g(a=0)=e.
Si vamos más allá podemos incluso hacer la identificación ya mencionada de los elementos del grupo, g(a), con la propia variedad, a. Se puede pensar así un grupo de Lie de orden r como el conjunto de transformaciones:
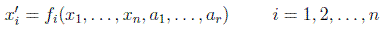
en donde n representa la dimensión del espacio sobre el que actúa y podemos reescribir por simplicidad como:
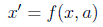
Estas transformaciones, lógicamente, deben cumplir las reglas de los grupos continuos. Por ejemplo, existirá un elemento inverso a-1 de forma que
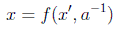
como podemos ver en el siguiente ejemplo de un grupo de orden 2 definido por la transformación:

cuyos elementos podemos denotar como (a1,a2) y cuyo producto podemos calcular como
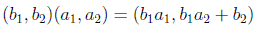
siendo la identidad el elemento (1,0) y el elemento inverso:
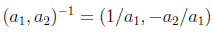
como se puede comprobar despejando la x.
Como se ha dicho, si utilizamos parámetros normales se debe cumplir que
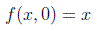
Si hacemos una transformación infinitesimal de coordenadas inducida por un cambio de parámetros del grupo obtenemos:
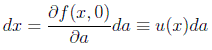
o de forma más general

en donde el índice griego recorre la variación a lo largo de todos los parámetros del grupo hasta r.
Si aplicamos esto a cualquier función F de las coordenadas obtenemos
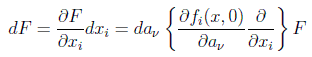
en los grupos de Lie al término entre llaves es lo que se suele llamar generadores del grupo, y habrá uno por cada parámetro esencial, es decir, se trata de un operador vectorial r-dimensional:
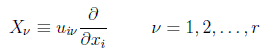
donde la suma recorre las dimensiones de la variedad hasta n.
El hecho de llamarlos generadores queda claro en la expresión:
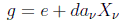
que representará el comportamiento del grupo en torno a la identidad en el llamado espacio tangente a la variedad diferenciable que definen sus transformaciones.
Este espacio tangente es el llamado álgebra de Lie del grupo y se trata de un espacio vectorial cuya dimensión es el orden del grupo por definición.
Lógicamente los generadores dependerán de la elección de los parámetros del grupo.
Vamos a indagar en las propiedades de este álgebra. Si nos preguntamos ahora por los elementos conjugados de g' respecto de un elemento dado g tendrán la forma:
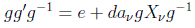
que corresponderían a un subgrupo que tuviera como generadores:
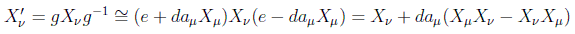
pero el primer miembro, al ser inducido por una transformación lineal de los parámetros, será una combinación lineal de generadores, y por independencia lineal también se puede afirmar que lo es el conmutador:

donde cμνλ son números complejos llamados constantes de estructura.
Debido a la independencia lineal se puede afirmar que las constantes de estructura cumplen una ley de anticonmutatividad:
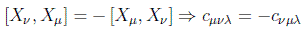
y asimismo se cumplirá la identidad de Jacobi:
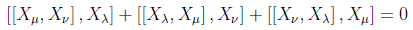
es decir
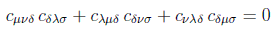
De esta forma, vemos cómo el espacio tangente definido por los generadores del grupo es un álgebra de Lie, pero esta definición es ampliable para cualquier espacio vectorial L que verifique las siguientes propiedades:
1) Existe una ley de composición llamada conmutador tal que

lineal en ambos argumentos.
2)
Se cumple la identidad de Jacobi para cualesquiera tres
elementos:
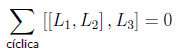
Si los conmutadores se anulan hablaremos de un álgebra abeliana. Si H es un subespacio lineal de L que es también álgebra de Lie, diremos que es invariante si para todo h en H, l en L, se cumple que [h,l] sigue perteneciendo a H. Diremos que es simple si no tiene subálgebras invariantes propias y semisimple si no tiene subálgebras invariantes propias no abelianas.
Ejemplo
Sea el grupo de orden 2 sobre un espacio de dimensión 1 siguiente:
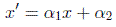
Primero reparametrizamos el grupo para que el elemento identidad sea el cero (parámetros normales):

recordando nuestra notación:
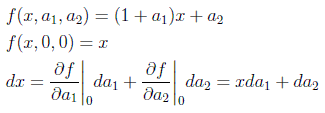
Por tanto los generadores son
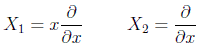
Veamos los que vale el conmutador

y por tanto las constantes de estructura del grupo son:
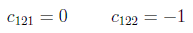
Una representación lineal D(g) de un grupo G es un homomorfismo de G sobre un grupo de operadores lineales actuando sobre un espacio vectorial V que recibe el nombre de espacio soporte de la representación y nos definirá la dimensión de la representación.
Si los operadores lineales son matrices hablaremos de una representación matricial.
Si la representación es un isomorfismo hablaremos de representación fiel (o exacta), por ejemplo, todos los grupos de matrices son representaciones fieles de ellos mismos. La representación trivial en la que D(g)=1 para cualquier elemento del grupo no es fiel (no es isomorfismo).
Si la representación consiste en matrices unitarias D(g)+=D(g)-1 se hablará de representación unitaria. Dos representaciones son equivalentes si se transforman entre sí por medio de una transformación de similaridad (o semejanza):
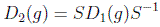
que constituye una relación de equivalencia. El operador lineal S deja invariante el álgebra en el sistema transformado:
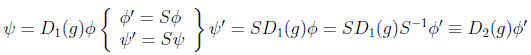
Una transformación unitaria es un caso particular de transformación de similaridad. De hecho, un importante teorema demuestra que cualquier representación de un grupo finito o matricial de un grupo de Lie se transforma semejantemente en una unitaria, por tanto cuando nos restrinjamos a las transformaciones unitarias no perderemos generalidad.
Si G es un grupo de matrices, se denomina representación fundamental a aquella definida por la acción natural de las matrices sobre el espacio vectorial, es decir D(g)v=gv. Por ejemplo, el grupo de rotaciones SO(2) tiene una representación fundamental en el espacio de dos dimensiones consistente en las conocidas matrices de rotación respecto a XY:
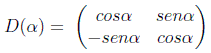
pero también tiene otra de dimensión 3 sobre el espacio tridimensional:
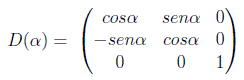
o incluso una no matricial sobre el cuerpo complejo:
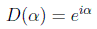
Sea una representación D(g) de un grupo en un espacio Vn. Si existe un subespacio Vk (k < n) que sea invariante (o estable) respecto a todas las transformaciones D(g), es decir:
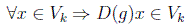
entonces la representación se denomina parcialmente reducible, y se puede encontrar una base de Vn en la que la representación tenga la forma:
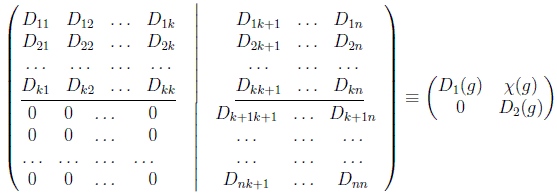
simplemente eligiendo los primeros k vectores columna como base de Vk y completando hasta lograr una base de Vn.
Cuando la representación no es reducible se denomina irreducible. No obstante en el caso unitario también se puede encontrar una transformación de similaridad que nos dé una representación totalmente irreducible, de la forma:
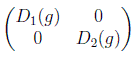
o como se conoce normalmente, diagonal por bloques. Esto se puede hacer siempre que la representación reducible sea unitaria. Basta con trabajar también con el subespacio suplementario o complemento ortogonal Vn-k:
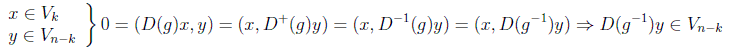
y como el inverso también puede recorrer todo el grupo, en este caso Vn-k también es invariante y se podrá encontrar la forma indicada.
En el caso de los grupos compactos toda representación reducible es totalmente reducible y se dice que se puede descomponer en suma directa de representaciones:
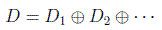
Un resultado que se utilizará mucho es el llamado lema de Schur, que afirma que una matriz que conmuta con todas las matrices de una representación irreducible es múltiplo de la identidad.
Un conjunto de números que nos proporcionan información sobre cada una de las clases de equivalencia de las representaciones son los caracteres de una representación, χ(g), que se definen como las trazas de las matrices de la representación. Todas las representaciones equivalentes tienen el mismo conjunto de caracteres. Esto es obviamente consecuencia de la ciclicidad de la traza que no se ve afectada por transformaciones de similaridad.
Como ejemplo estudiemos la paridad P en 2D o reflexión respecto a la identidad. Esta operación tiene como generadores e y p, siendo su representación fundamental:
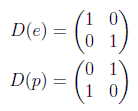
Si escogemos como matriz de similaridad una rotación de 45º:
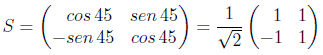
obtenemos una representación equivalente
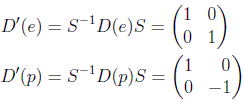
vemos que las trazas son las mismas, representan los caracteres de la representación. Además la representación se puede poner como suma directa de dos representaciones actuando en dos subespacios, de los cuales en este caso sólo interesa el segundo, que corresponde a la paridad par o impar dependiendo únicamente de un signo aplicado a la segunda coordenada.
Los vectores base de una representación unitaria irreducible correspondiente a una transformación de simetría nos definen una serie de estados mecánicos denominados multipletes.
En efecto, si consideramos una función dinámica, que normalmente como veremos será el llamado hamiltoniano, invariante bajo una transformación unitaria U(a) se cumple, para un autoestado φn del hamiltoniano:
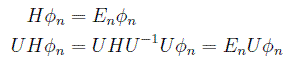
en donde hemos hecho la manipulación habitual de introducir la identidad. De esta forma se puede decir que bajo la transformación:
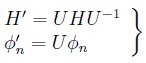
y dado que hemos supuesto el hamiltoniano invariante bajo la transformación U (H'=H), se obtiene el resultado:
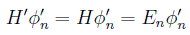
Lo que representa un conjunto de estados φ'n para cada parámetro del grupo a que tienen la misma energía. En este caso se dice que los estados están degenerados, y la representación correspondiente será forzosamente irreducible de modo que no se puedan mezclar estados con energías distintas. Este es uno de los motivos más importantes para descomponer una representación en sus partes irreducibles.