
INFORMACIÓN CUÁNTICA

Antes de pasar al tema de computación cuántica, tan de actualidad en estos días (2011), debemos primero pararnos a analizar en qué consiste la información cuántica, la otra gran rama dentro de este contexto. En efecto, la computación estará relacionada con el procesado y el cálculo de la información, la cual a su vez está relacionada con la comunicación y el almacenaje.
Debemos hacer antes una reflexión epistemológica. Hasta ahora la teoría de la información era tratada generalmente al margen de la Física, en facultades e ingenierías informáticas. Sin embargo la información se transmite físicamente (ondas, corrientes...) y se guarda en soportes físicos (ya sea un cerebro, un papel o un disco duro). De esta interconexión tan estrecha ya empezó a darse cuenta el mismo Feynman en los años 80, aunque fue en los 90, después de su triste pérdida, cuando estalló el boom de la información cuántica. La información está sometida, pues, a las leyes de la Física y puede afirmarse con Landauer (1991) que la información tiene naturaleza física.
Si se cumple la función experimental de Gordon Moore, los dispositivos electrónicos básicos de los microchips llegarán al límite atómico-molecular en menos de 20 años, y empezarán a ese nivel a notarse los efectos cuánticos. Las ventajas que ofrecerían los ordenadores basados en la lógica del bit cuántico (qubit) son incuestionables. Así como el número de estados codificables con N bits es 2N, el número de estados con N qubits será infinito, ya que en principio los valores posibles estarán relacionados con las distintas combinaciones lineales de una base (superposición lineal). Con unos cientos de qubits se podría acumular tal información que con bits no cabría en todo el Universo. Además gracias a este principio de superposición, cuánticamente se pueden hacer multitud de operaciones al tiempo (paralelismo masivo). Por contra, aunque la información guardada en bits es robusta, la información guardada en qubits es sumamente frágil (decoherencia) y hay que tener extremo cuidado a la hora de medir. Asimismo, aunque la información guardada en bits se puede copiar cuantas veces se quiera, se ha demostrado la imposibilidad de clonación exacta de estados cuánticos no ortogonales. Pero esta desventaja también ofrece su lado bueno, ya que teóricamente nos ofrece la posibilidad de algoritmos de encriptación absolutamente infalibles (entrelazamiento), al contrario de lo que ocurre con los bits, en los que todo algoritmo es susceptible de ser crackeado (criptografía). De hecho en la actualidad (2011) la criptografía cuántica ha alcanzado un estatus comercial, aunque sigue teniendo muchas limitaciones de distancia por el hecho de la degradación de la información y que no se puedan construir "repetidores" clásicos por el teorema de no-clonación.
La unidad para medir la información de un sistema clásico, introducida por Claude Elwood Shannon, es el bit (también llamado cbit, por bit clásico). El nombre de bit, por binary digit, así como el de software, se debe a John Wilder Tukey. Así un sistema como la tirada al azar de una moneda ideal contendría un bit de información, y se representaría por dos valores 0 ó 1, según saliera una cara u otra (el caso en el que cayera de canto es tan improbable que ni siquiera se contemplaría).
En el caso de un sistema más complejo, como por ejemplo varias monedas distintas, tendríamos un sistema multibit, compuesto por una serie de resultados consistentes en ceros y unos:
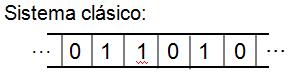
El número de estados, configuraciones o resultados posibles para n bits será por tanto:
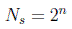
o, a la inversa, podemos definir el número de bits de un sistema como la cantidad:
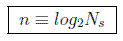
con lo que obtendremos el número de bits para cualquier sistema. Por ejemplo, en el caso de la tirada de un dado, que tiene Ns=6 estados, el número de bits sería aproximadamente 2'6, es decir, no tiene por qué ser entero. Y así se puede generalizar para cualquier magnitud física, por ejemplo la temperatura en un recinto dividido en pequeños cubos de temperatura constante podría ser expresada en bits asociando a cada cubo su valor de la temperatura en binario.
De esta forma, si conocemos cómo evolucionan los bits en cada sistema, conoceremos cómo funciona su física.
La unidad de información cuántica es el qubit (o qbit, por quantum bit), término acuñado por Benjamin Schumacher en 1995. Se trata de la unidad de información que posee un sistema cuántico cuya base de Hamel es 2, es decir, con dos estados base o configuraciones relevantes. El ejemplo típico de esto es el spin del electron, aunque también se suele usar la dirección de polarización de un fotón o los niveles de excitación de un átomo.
El espacio de Hilbert de un qubit es isomorfo a C2. Si denotamos por |0 > y |1 > a los estados base, vemos que el qubit puede estar en los infinitos estados de la forma:
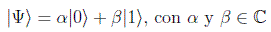
que son estados puros o superposiciones lineales coherentes de los estados base. En principio por tanto tendría 4 grados de libertad reales, pero la irrelevancia de la fase global y la condición de normalización hace que podamos poner el estado en la forma:
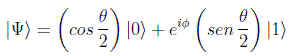
en donde θ y φ son los ángulos esféricos que representan un punto en la llamada esfera de Bloch:
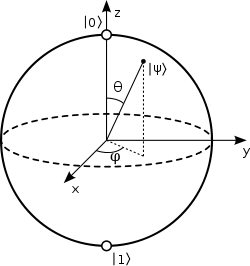
Y por tanto el espacio de Hilbert de esos estados puros se asociará con un punto en esa esfera y un sistema multiqubit será algo como lo expresado en la figura siguiente:
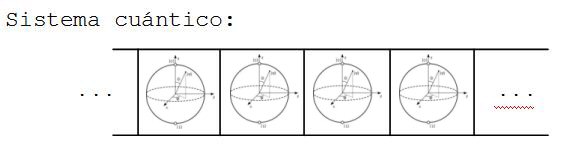
El espacio de Hilbert para n qubits será entonces
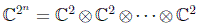
y sus vectores base naturales se denotarán como:
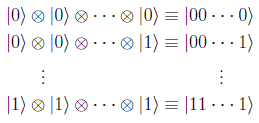
denominada base computacional, y en donde no se utiliza el orden numérico sino el llamado orden lexicográfico. A veces para abreviar se utiliza la notación decimal, es decir, se expresa |x > en lugar del vector |xn-1 ··· x0 > si su descomposición binaria es efectivamente x=2n-1xn-1+··· +2x1+x0 y por tanto tendríamos |9 >=|1001 >.