
COMPUTACIÓN CUÁNTICA

Aunque las primeras máquinas mecánicas de calcular se deben a Schickard, Pascal y Leibnitz en el siglo XVII, no fue hasta poco después de la primera revolución industrial en el siglo XIX cuando se produjo un salto cualitativo y el matemático británico Charles Babbage, inspirado por el telar de Joseph-Marie Jacquard, puso a punto, al menos en teoría, la primera calculadora automática digital de uso general, la Máquina Analítica. Era el año 1834.
Los mejores estudios sobre la Máquina Analítica los dio Ada Augusta, condesa de Lovelace, "la única hija de la casa y el corazón" del poeta Byron. Hoy en día es considerada la primera programadora de la historia y el lenguaje de programación ADA, relacionado con la seguridad aeronáutica, debe a ella su nombre.
Aunque hubo después más autores de trabajos interesantes sobre el automatismo, entre los que figura en buena posición el ingeniero cántabro Leonardo Torres Quevedo, el trabajo de Babbage fue olvidado hasta los años cuarenta del siglo XX, cuando otra generación de científicos e ingenieros, luchando de nuevo con el problema de diseñar calculadoras digitales de gran escala, llegaron a darse cuenta de que Babbage, con todos sus engranajes y bielas se les había anticipado.
El principal artífice del nuevo impulso fue el brillante matemático inglés Alan Mathison Turing, creando una abstracción mental de un ordenador tan profunda que entraña los principios generales de cualquier calculador que haya sido construído jamás, la máquina de Turing.
La primera materialización electrónica de esta máquina fue el computador ENIAC, "Integrador y calculador numérico electrónico", desarrollado por la Universidad de Pennsylvania en 1946. Una máquina de 30 toneladas con un rendimiento de 200000 flops (operaciones de coma flotante por segundo). Hoy en día ese rendimiento lo alcanza cualquier calculadora de bolsillo. De hecho, los superordenadores actuales alcanzan rendimientos de decenas de petaflops, es decir, decenas de miles de billones de operaciones por segundo (concretamente al escribir estas líneas el record lo tenía el ordenador CRAY XK6 o Interlagos de la empresa americana Cray Inc., con 50 Pflops de rendimiento).
Hubo que esperar a los años ochenta para que surgiera la generalización de la máquina de Turing al caso cuántico (Deutsch, Benioff) como máquinas reversibles y a la primera propuesta de ordenador cuántico (Feynman). Una década más tarde surgieron los primeros algoritmos de cálculo eminentemente cuánticos, como el de Shor (1994) o el de Grover (1996). También en esta época empezaron a darse los primeros experimentos para implementar qubits y puertas lógicas, como los iones atrapados de Cirac y Zoller en 1995 o los experimentos de resonancia magnética nuclear de Gershenfeld y Chuang en 1997.
En la actualidad se manejan sistemas cuánticos cada vez más ambiciosos, la empresa IBM junto con la Universidad de Stanford ha implementado el algoritmo de Shor en el primer computador cuántico de 7 qbits, la Universidad de Innsbruck creó el primer qbyte con trampas de iones y se están desarrolllando los primeros buses y procesadores cuánticos, , aunque parece que aún queda bastante para nuestro ansiado computador (2011).
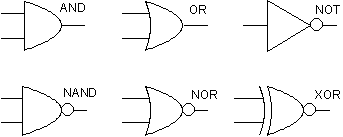
Las máquinas de Turing son equivalentes a circuitos lógicos en donde se le realizan procedimientos no triviales a la información. Estos procedimientos se denominan puertas lógicas. Normalmente estas puertas poseen en electrónica una representación normalizada, como se muestra en la figura.
El ejemplo más básico de puerta es la unaria (o monaria) que representa la negacion, NOT, que pueden hacer por ejemplo los transistores sobre corrientes eléctricas, y cuya tabla de verdad y representación esquemática es como en la figura siguiente:
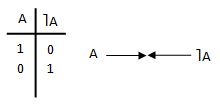
, y cuyo significado es obvio, si entra corriente no sale y si no entra sale.
Esta primera puerta lógica se puede usar tanto clásica como cuánticamente, ya que es reversible, es decir, siempre se puede recuperar el estado inicial conocido su producto. Por el principio de Landauer, esta puerta no disiparía calor. En el formalismo cuántico se suele representar esta puerta como:

Como hemos dicho, las puertas lógicas clásicas se implementan con elementos no lineales como los transistores. En el caso cuántico, las puertas lógicas deben representarse mediante operadores unitarios U que se consiguen en la práctica con interacciones reversibles entre los elementos cuánticos. Recuérdese que en el caso cuántico no sólo se actúa sobre dos posibles estados del bit, sino sobre los infinitos estados del qubit.
Existen 4 puertas unarias, de las cuales sólo dos son reversibles, la identidad y la puerta NOT estudiada. Las otras dos serían las asignaciones A->1 y A->0, que al ser irreversibles no serían implementables cuánticamente, a no ser que se añada la información del qubit entrante en el producto.
El operador unitario correspondiente a NOT en la base estándar será:
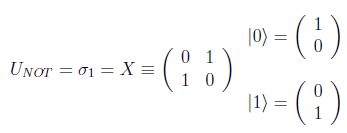
Veamos lo que ocurre para un qubit de información entrante |Ψs >, que en general tendrá la forma:
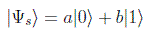
observando que, básicamente, se trata de una reflexión sobre la identidad, en la que el caso clásico (el cambio de 0´s y 1´s) es sólo un caso particular:
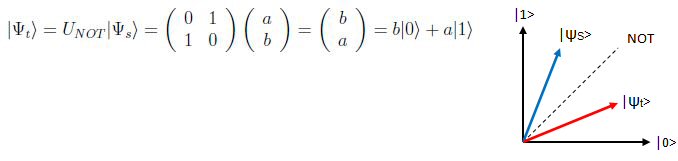
Se puede hacer una interpretación en el contexto de los operadores fermiónicos en donde la base elegida correspondería a los estados cero y uno de una partícula (o fundamental y excitado). De esta forma el operador NOT sería la suma de los operadores de destrucción y creación:
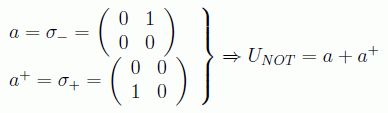
La condición de reversibilidad se puede comprobar
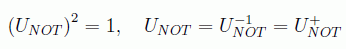
Todas las puertas lógicas clásicas son susceptibles de ser implementadas también cuánticamente. La extensión de las puertas lógicas a la teoría cuántica se debe a David Deutsch (1985).
Cuánticamente cualquier matriz unitaria define una puerta cuántica válida, la mayoría sin contrapartida cuántica. Como ejemplo de puertas lógicas unarias cuánticas estaría el resto de las matrices de Pauli:
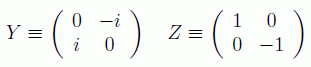
en donde la actuación de Z es fácil de interpretar, ya que deja el estado fundamental inalterado y cambia el signo del excitado.
Otra puerta cuántica relevante es la de Hadamard (en honor al matemático francés Jacques Hadamard):
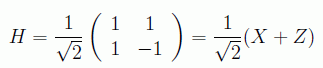
Esta puerta mezcla los estados equiprobablemente poniéndolos como suma y diferencia:
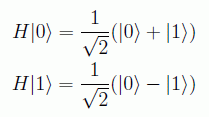
Recordando que en la esfera de Bloch se puede poner el estado como:
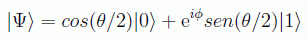
en donde θ es el radio entre |0> y |1> y φ una fase cuántica. En la esfera de Bloch por tanto, si se parte del estado:
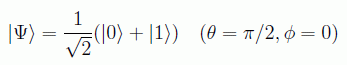
y se aplica el operador de Hadamard, se llega al estado fundamental:
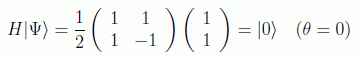
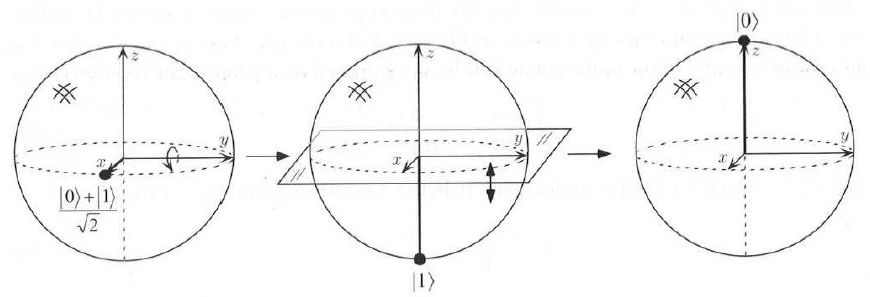
es decir, se produce una rotación sobre el eje y de 90º seguido de una de 180º sobre x (figura). El operador de Hadamard es una de las puertas cuánticas de mayor utilidad ya que realiza lo que se conoce como paralelismo masivo, ya que un estado de n qubits lo pone en superposición de 2n estados. Por ejemplo, para n=2:
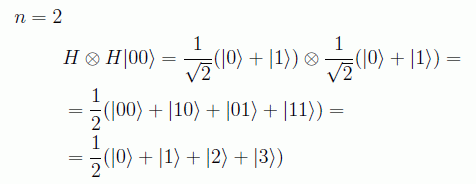
en donde se ha utilizado la conversión a decimal ya explicada en el capítulo anterior. En general, cuando el operador de Hadamard se aplica n veces, se habla del operador de Walsh-Hadamard, en honor del matemático americano Joseph Leonard Walsh:
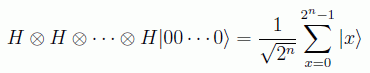
Otra de las puertas monarias eminentemente cuánticas sería la raiz de NOT:
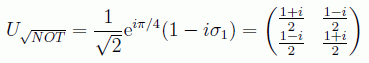
Y también está la puerta de corrimiento de fase:
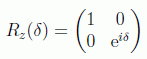
esta puerta genera una rotación en dirección contraria a la aguja del reloj respecto al eje z de la esfera de Bloch. Una rotación en general se puede poner, con ayuda de las matrices de Pauli (usando su nilpotencia-2), en la forma:
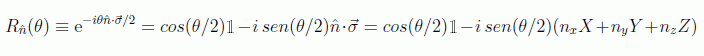
En realidad se puede dar una expresión para las infinitas puertas cuánticas monarias, por ejemplo la correspondencia a la descomposición de las matrices 2x2:
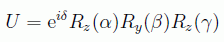
en donde δ es la fase (mod π) del factor de U(2) y α,β y γ son los ángulos de Euler que parametrizan el factor de SU(2):
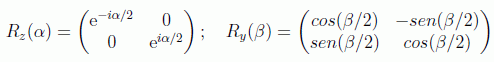
A partir de esto se puede obtener otra descomposición interesante:
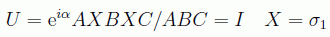
de forma que
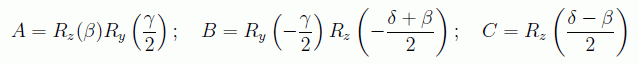
Vamos a estudiar ahora las puertas de múltiples qubits, las más sencillas de las cuales son las puertas binarias, aunque su implementación en el laboratorio es extremadamente difícil, pues hay que poner en interacción controlada dos qubits espacialmente separados. Cirac y Zoller lo hicieron con iones fríos en una trampa lineal.
En general hay 256 puertas binarias. De hecho el número de puertas cuánticas que hay m x n es

ya que es el número de funciones del tipo
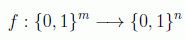
Sin embargo puertas reversibles solo hay

que es el número de funciones del tipo anterior que además son invertibles. Por tanto habrá 24 puertas binarias reversibles. En general las puertas son implementadas por matrices 2mx 2m. En el caso binario la base computacional es:
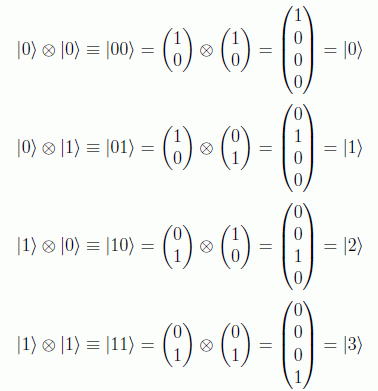
De las puertas binarias podemos destacar la puerta NOT-controlado, CNOT, en donde se distingue el primer qubit como de control y el segundo como blanco. Si el primer qubit es 0 el segundo se deja intacto, y si es 1 se cambia:
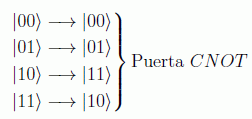
Otra forma de ver esta puerta es relacionándola con la puerta clásica del OR exclusivo, XOR, ya que es precisamente el segundo qubit el que nos da los valores de XOR, que coinciden con la suma módulo 2 que representamos con ⊕:
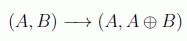
o mediante el gráfico
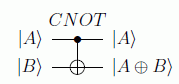
La expresión matricial de XOR es fácil de construir sabiendo que cada una de las columnas debe transformar |00>,|01>,|10> y |11>, de modo que
La puerta CNOT se puede implementar con una molécula de cloroformo CHCl3. Su estado corresponde a los estados de espín de los núcleos de carbono e hidrógeno, que invierten su sentido mediante pulsos de ondas de radio. Siempre es posible asegurarse de que el núcleo de hidrógeno invierte su espín sólo cuando el espín del núcleo de carbono apunta hacia arriba (el núcleo de carbono sería el control y el de hidrógeno la puerta XOR).
Nótese que la puerta XOR clásica sería irreversible (no invertible), dado que su tabla de verdad no nos permite, conociendo el resultado, deducir los estados iniciales. Se produce pérdida de información. En cambio como puerta cuántica unitaria siempre será invertible.
La puerta CNOT es de gran importancia, ya que como veremos cualquier puerta de múltiples qubits puede ser construida mediante la puerta CNOT y puertas cuánticas monarias.
Además, para implementar proposiciones del tipo "Si A es verdadero, entonces haz B", son útiles las llamadas operaciones controladas, basadas en el mismo principio que CNOT. Se trata de puertas binarias U-controladas, es decir, que al qubit blanco se le aplica U dependiendo del valor del qubit de control. Esto se puede denotar como
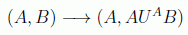
o bien gráficamente
y en el caso en que el operador se tenga que hacer cuando el primer bit está a cero se utiliza el esquema:
Por ejemplo otra puerta binaria muy conocida es la del corrimiento de fase controlado, CPHASE:
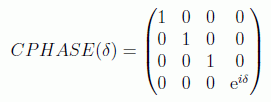
cuando δ=π se tiene la puerta CMINUS.
En los años 80 Tommaso Toffoli y Edward Fredkin vieron que hacía falta un mínimo de tres qubits para cualquier computación clásica. La extensión a tres qubits de la puerta CNOT es la llamada puerta de Toffoli o CCNOT. En este caso hay dos bits de control que sólo actúan si están a 1.
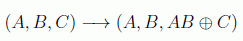
es fácil ver que al hacerla actuar dos veces se consigue la identidad, luego es también una puerta reversible (su inversa es ella misma). La expresión matricial en este caso sería:
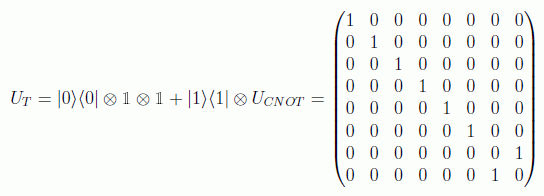
y gráficamente
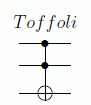
Esta puerta se suele usar para simular puertas clásicas irreversibles y demostrar que cualquier ordenador cuántico puede hacer lo mismo que uno clásico. Entre su singularidad está el que en sus tripas está una de las puertas clásicas más importantes, la puerta NAND (NOT AND). Sucede cuando el tercer bit es uno, ya que se reproduce la tabla de verdad del NAND:
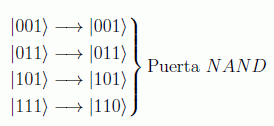
dicho de otra forma:
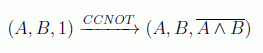
Otra puerta interesante es la que intercambia los estados de dos qubits, en el caso binario es la puerta intercambiadora o SWAP:
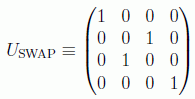
y en el ternario se denomina intercambiador controlado o puerta de Fredkin:
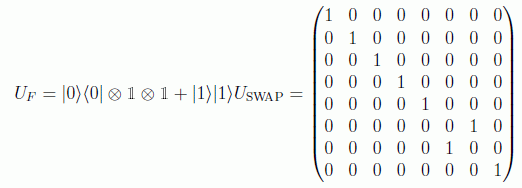
o gráficamente
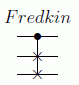
Además, siempre podemos definir operaciones controladas sobre estados de múltiples qubits. Si por ejemplo tenemos n+k qubits y U es un operador unitario que actúa sobre k qubits, podemos definir la operación controlada Cn(U) como
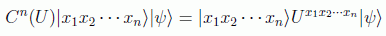
y por tanto U sólo se aplica si los n primeros qubits son iguales a 1.
El teorema de no clonación, introducido independientemente por William Wootters y Wojciech Zurek por un lado y por Dennis Dieks por otro (este último relacionándolo con la causalidad relativista) en 1982, afirma que de acuerdo con las propiedades unitarias de la mecánica cuántica, no es posible hacer una copia o clonación de un estado cuántico arbitrario.
Lo que se afirma por tanto es que no existe la puerta cuántica:
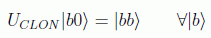
En efecto, consideremos el estado general:
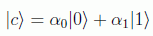
Aplicando la linealidad tendremos
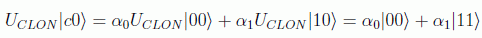
y por otra parte
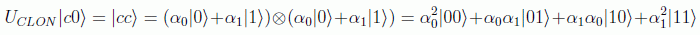
el cual es un estado en general distinto a no ser que una de las dos amplitudes sea nula.
Por tanto, hemos probado, sólo admitiendo la linealidad de la MC, que no es posible clonar un estado cuántico arbitrario. Se puede ver además que la unitariedad implica que no se pueden clonar dos estados cuánticos distintos y no ortogonales. En efecto, sean los estados a clonar ψ y φ y el estado auxiliar χ, de forma que:
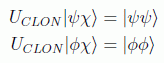
y hagamos el producto escalar de las dos igualdades miembro a miembro:
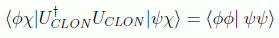
aplicando la unitariedad se tiene
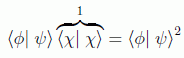
es decir
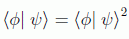
lo cual sólo es cierto si φ=ψ (estados iguales) o si su producto escalar es cero (estados ortogonales).
La simplicidad de este teorema desconcertó a la comunidad científica, que no entendió cómo pudo pasar inadvertido durante tantos años.
Es cierto que este hecho, aunque tiene la grave desventaja en computación cuántica relacionada con las lecturas y las copias de seguridad, es de una gran importancia en criptografía cuántica.
Además, el teorema no impide la copia exacta de un estado conocido, y tampoco el hecho de que se puedan construir algoritmos de copia aproximados (Vladimir Buzek, Mark Hillery, 1996). Esto tampoco impide la teleportación de estados, en donde es borrado el estado original.
Clásicamente un ordenador se define como una cinta finita dividida en n estados (celdas) con un estado inicial y otro final distinguibles. Además las celdas son descritas mediante cierto alfabeto y habrá una cabeza que lea y escriba ese alfabeto, dirigida por una unidad de control que dicta ciertas reglas. Cuando la unidad de control alcanza un estado final se para.
En computación clásica los estados vienen representados por bits. En computación cuántica el estado viene representado por un vector del espacio de Hilbert:
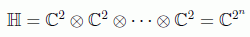
para un estado de n qubits. Es decir, un vector será de la forma:
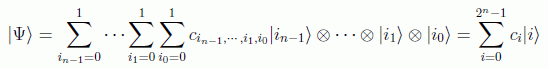
con
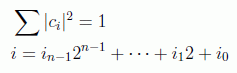
La diferencia principal con el caso clásico estriba en el principio de superposición. Si tenemos n bits podemos almacenar un solo entero de entre los 2n posibles. Sin embargo, con n qubits, gracias al principio de superposición podemos formar infinitos estados, cualquier combinación lineal de los 2n estados base, y su especificación requiere conocer 2n amplitudes (para n=300 ese número es del orden del número de grados de libertad del universo visible). Esto hace que mientras en un ordenador clásico su capacidad de memoria sea linealmente proporcional a su tamaño, en uno cuántico habría dependencia exponencial.
Así como en computación clásica hay un teorema que establece la equivalencia entre máquinas de Turing y circuitos lógicos, curiosamente establecido en los años 70 (Savage, Schnorr, Fischer), mucho después de la construcción de los primeros ordenadores, en el caso cuántico hay un resultado similar de 1993 debido a Andrew Chi-Chih Yao, mostrando que la máquina de Turing cuántica se puede reducir al estudio de los circuitos cuánticos. Para cualquier cómputo cuántico se necesita:
1) Preparar un estado inicial |Ψi>.
2) Manipularlo mediante transformaciones unitarias |Ψf>=U|Ψi>.
3) Realizar una medición en nuestra base computacional (por ejemplo medir la polarización a lo largo del eje z mediante el operador de Pauli σz de cada uno de los qubits).
El proceso de medida convierte un estado simple de un qubit |Ψ>=α|0>+β|1> en un bit clásico R que será cero con probabilidad |α|2 ó 1 con probabilidad |β|2. Gráficamente:
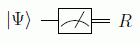
El fenómeno del entrelazamiento, puramente cuántico, viene a decir que los estados cuánticos de dos o más partículas se deben describir haciendo referencia a los estados de todos los objetos del sistema, sin importar que estén separados espacialmente.
Si los estados de dos partículas se definen por los subespacios H1 y H2, un estado general del sistema no será de la forma
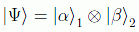
en cuyo caso diríamos que es separable, sino un estado entrelazado, es decir, una combinación lineal del tipo:
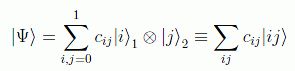
Por ejemplo el estado
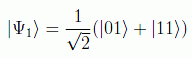
sería separable, ya que
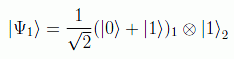
Ejemplos clásicos de estados entrelazados son los estados de Bell:
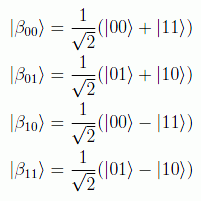
en donde la notación nos permite usar la forma abreviada
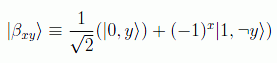
Se puede diseñar un circuito para obtener estos estados a partir de los de la base. Por ejemplo:
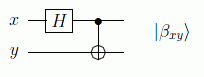
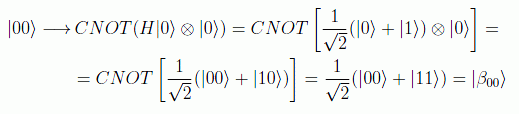
y de la misma forma se generan los demás
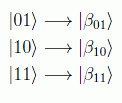
El mayor poder de cálculo en el terreno cuántico es originado por el llamado paralelismo cuántico, consecuencia a su vez de la superposición cuántica, que nos permitiría conocer los resultados de varias operaciones simultáneamente.
En 1995, los profesores de la Universidad de Oxford Vlatko Vedral, Artur Ekert y Adriano Barenco publicaron diferentes formas con las que se podían hacer operaciones clásicas cuánticamente. Veamos cómo se podrían realizar sumas simultáneas con una única unidad de control.
Recordemos primero cómo se hacían las sumas en binario (módulo 2):
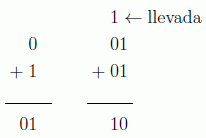
En el caso cuántico para las sumas de dos bits utilizamos la puerta de Toffoli con el tercer qubit a cero y la puerta CNOT:
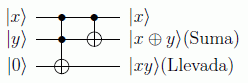
Si preparamos el primer estado como superposición en teoría podríamos hacer dos sumas simultáneamente:
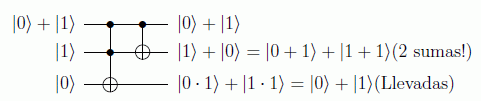
El fenómeno de interferencia se puede ilustrar con la aplicación de la puerta de Hadamard a un quibit arbitrario:
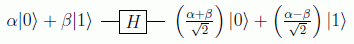
Se observa que en un caso las probabilidades se suman (interferencia constructiva) y en el otro se restan (interferencia destructiva). El caso extremo es aquel en el que:
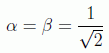
en donde se tiene que el estado |0> pasa de tener 50% de probabilidades de aparecer a la certeza absoluta de encontrarlo después de la medición, cuando ya no se podrá encontrar el estado |1>.
En computación clásica un teorema importante afirma que cualquier función sobre bits puede ser evaluada mediante la composición de puertas NAND únicamente, ya que como consecuencia de las leyes de Morgan (en honor del lógico inglés Augustus De Morgan), si denotamos con ↑ a la operación NAND se puede probar que:
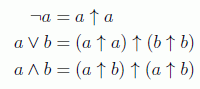
Esto implica que en computación cuántica nos bastaría con la puerta de Toffoli para evaluar funciones clásicamente. Es por esto que se dice que la puerta NAND es universal. En realidad si se habla de conjuntos universales, en este caso la mencionada puerta, para de verdad emular un verdadero computador, debería ir acompañada de la puerta COPY o FANOUT que copie estados, definida como:
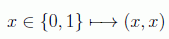
En computación cuántica se dice que un conjunto de puertas es universal si cualquier operación unitaria puede ser aproximada con precisión arbitraria por un circuito cuántico construido con esas puertas. La puerta de Toffoli no es ya universal en computación cuántica.
Fue David Deutsch en 1989 el primero que mostró la existencia de una puerta universal cuántica, la puerta de Deutsch, de tres qubits. Se trata de una generalización de la puerta de Toffoli del tipo:

Como se ve, se trata en realidad de una familia de puertas. Además, debido al hecho de que D(α)D(α')=iD(α+α'), se suele fijar α como un múltiplo irracional de π, de forma que una puerta pueda generar todas las demás asintóticamente. Además, la equivalencia
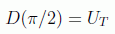
asegura que cualquier cálculo clásico se puede hacer también con un circuito cuántico.
En 1994 David DiVicenzo descubrió que la puerta de Deutsch podía descomponerse en puertas binarias, lo cual fue una sorpresa, dado que la lógica clásica reversible requiere puertas ternarias para la universalidad. Ya comentamos que Toffoli y Fredkin observaron que hacían falta puertas ternarias para la lógica clásica reversible. Sin embargo, la puerta de Toffoli (y cualquiera) puede ser descompuesta en puertas binarias y monarias con la ayuda de las características eminentemente cuánticas, lo que implica el sorprendente resultado de que sólo son necesarios dos qubits para la lógica cuántica.
Vamos a desarrollar esto un poco más. Veamos por qué son necesarios tres bits en lógica clásica reversible. Imaginemos que queremos implementar la puerta universal NAND con solo dos bits. Para hacerla invertible deberíamos poner el resultado en uno de los dos bits entrantes:
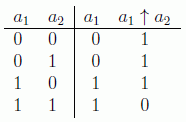
Como se ve, esto no nos valdría ya que perdemos la reversibilidad. Las dos primeras entradas producen la misma salida. Es necesario pues un tercer bit que nos dé información de la entrada.
Con puertas ternarias clásicas sin embargo siempre se pueden simular puertas de más bits. Vemos por ejemplo cómo se puede reducir la puerta cuaternaria CCC-NOT con puertas de Toffoli:
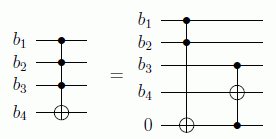
como se ve, se usa un bit auxiliar inicializado a 0, de forma que en él se escriba el resultado de los dos primeros bits, si están a 1 este también estará a 1 y nos servirá para aplicar un NOT al cuarto bit siempre que también esté el tercero encendido, como hacía la puerta original cuaternaria. Se ha reducido pues una puerta cuaternaria a dos puertas ternarias. Veamos ahora por qué no se puede reducir clásicamente una ternaria con binarias:
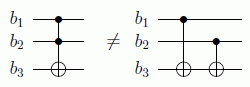
vemos que el NOT aquí sobre b3 se hace cuando uno de los dos bits son 1, no cuando lo son los dos. Sin embargo, con puertas eminentemente cuánticas sí se puede reducir el circuito ternario, en la forma:
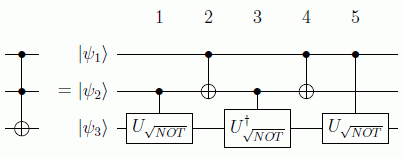
En donde ya hemos estudiado la raiz de NOT como puerta unitaria, la recordamos aqui en sus varias formas:
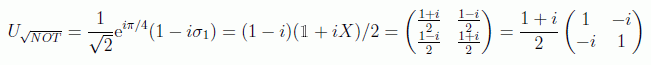
Para hacernos una idea de cómo actúan los circuitos, veamos en dos ejemplos cómo efectivamente las puertas binarias reprocucen la de Toffoli:
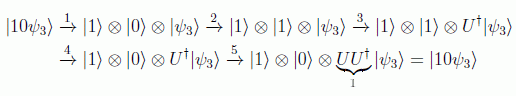
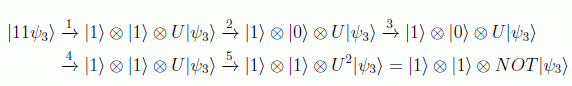
En realidad esto se puede extender a cualquier puerta C2-U, en donde siempre se tendrá la equivalencia:
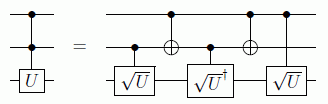
El resultado general mostrado por Adriano Barenco y otros que se apoyaron en trabajos anteriores fue que cualquier operación unitaria en el espacio de Hilbert H de n qubits puede descomponerse en una secuencia de puertas de 1 qubit y de 2 qubits CNOT. Este conjunto infinito además es exactamente universal. Existen sin embargo conjuntos discretos universales, como el formado por la puerta de Hadamard y la puerta de fase controlada.
Un algoritmo cuántico es un proceso encaminado a realizar alguna tarea computacional específica. Esto en la práctica supone extraer alguna de las amplitudes de los N qubits que forman parte de la computación. Recordemos que en efecto cualquier estado de un conjunto de N bits queda especificado por N bits mientras que para especificar N qubits necesitamos los 2N números que representan las amplitudes de superposición.
Aunque en teoría esto denota la mayor capacidad de cálculo de la computación cuántica, en la práctica esta información almacenada en las amplitudes permanece oculta, y la mayor parte se destruye en el proceso de medición, obteniendo sólo una pequeña parte. Aún así, la información extraída en un algoritmo suele ser de una utilidad y efectividad mucho mayor que la correspondiente al cálculo clásico.
Algunos de los algoritmos cuánticos más famosos son:
Algoritmo de Deutsch-Jozsa, o "cómo mirar las dos caras de la moneda a la vez".
Algoritmo de Simon, o "cómo averiguar, en tiempo polinómico, el periodo de una función".
Algoritmo de Shor, o "cómo factorizar en tiempo polinómico".
Algoritmo de Grover, o "cómo hallar una aguja en un pajar".
Por razones históricas el primero de los algoritmos a estudiar es el propuesto por David Deutsch en 1985. Aunque en el fondo no sea de una gran utilidad para casos prácticos, en él se empieza a apreciar el funcionamiento y la potencia de los programas cuánticos.
Antes debemos hacer algún comentario sobre la forma de evaluar una función en computación cuántica. Para asegurar la reversibilidad del proceso de evaluación, es necesario siempre un registro auxiliar en donde se guarde el resultado de la consulta auxiliar (a veces denominada query por contagio de los lenguajes de bases de datos) además de encontrarse también los valores iniciales en el registro de salida. Es decir, usaremos un registro dividido en dos, la fuente (source) y el destino (target):
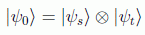
Para implementar una función booleana por tanto necesitaremos únicamente un qubit adicional que nos dé el resultado, el cual se puede evaluar fácilmente mediante la suma módulo 2 (⊕) , o, dicho de otra forma, el operador lógico XOR:
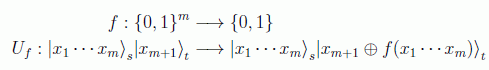
o gráficamente
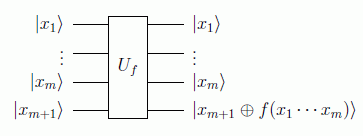
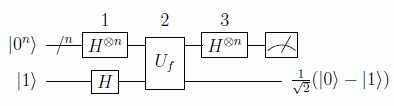
El problema de Deutsch trata de discernir, para m=1, si la función es constante o no con una sola pregunta. Es decir, una función puede que dé en una query f(0)=1, pero por esto no podemos afirmar, clásicamente, que la función sea constante, habrá que averiguar también cuánto vale f(1), es decir, hacer dos queries. Pues bien, usando adecuadamente el llamado a veces oráculo cuántico Uf (no deja de ser una puerta a la que se le hace una pregunta) se demuestra que con sólo una indagación en computación cuántica podemos averiguar el resultado. El circuito es el siguiente:
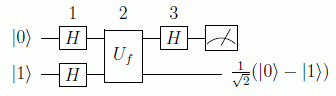
Vamos analizar el programa paso por paso. Antes recordemos la forma de actuar del operador de Hadamard:
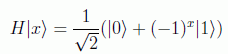
Partimos del estado inicial
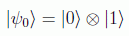
aplicamos los operadores de Hadamard:
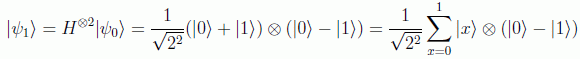
ahora haremos actuar el operador que implementa nuestra función, teniendo en cuenta que:
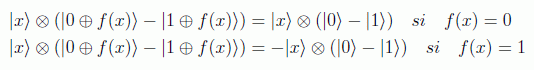
con lo que se podrá poner
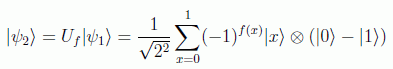
y por último el primer qubit pasa por una puerta de Hadamard:
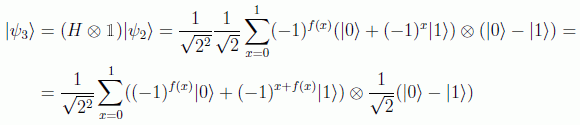
Sólo queda medir el primer qubit. Si está en el estado |0>, la función será constante, de lo contrario no. Esto es así debido al siguiente hecho:
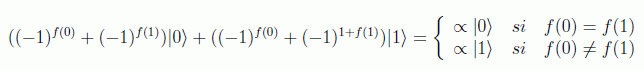
La generalización a funciones booleanas sobre n qubits la hizo Deutsch junto a Richard Jozsa en 1992. Ahora se trataba de ver si una función es constante o está equilibrada o balanceada, es decir, si es 0 para la mitad de las entradas y 1 para el resto. El circuito que se emplea es similar:
Ahora el estado inicial es de la forma:
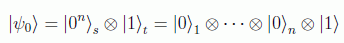
aplicando los operadores de Hadamard, recordando el resultado en notación decimal se obtiene:
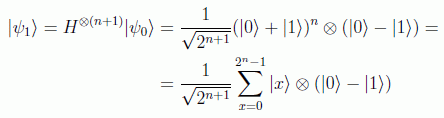
y después de pasar por la puerta funcional queda:
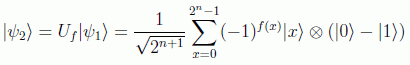
Para aplicar el operador de Hadamard sobre los n primeros estados hay que tener en cuenta el resultado:
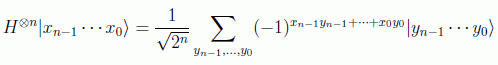
por ejemplo
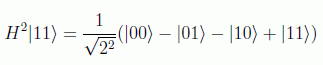
resultado que se puede compactar usando el producto escalar binario pero en notación decimal:
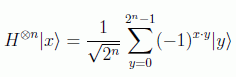
Usando el resultado obtenemos el estado final:
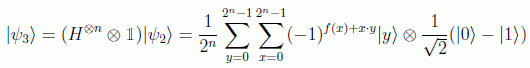
y de nuevo se puede obtener, con una sola medida, que si los primeros n qubits están en el estado |0n> con probabilidad 1, la función será constante, y si la probabilidad es 0, la función estará balanceada, en los restantes casos la función simplemente no sería constante. Como ilustración, los términos para n=2 para el primer qubit serían:
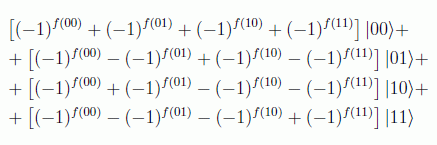
por tanto, con una sola query podemos adivinar la constancia o el balanceo de la función. Nótese que, si a priori sabemos que la función es constante o balanceada, clásicamente en teoría habría que hacer tres medidas para averiguar cuál de las dos opciones es, en el peor de los casos (en el mejor con dos nos valdría). En general en el peor de los casos habría que indagar en la mitad más uno de los posibles resultados, es decir, para una función de n bits habría que hacer 2n/2+1 queries, frente a dos si tenemos suerte o a uno si aplicamos la computación cuántica.
La primera implementación experimental de este algoritmo fue propuesta, para dos qubits, en 1998 por Jonathan Jones y Michele Mosca para técnicas de espines bajo resonancia magnética nuclear (RMN). Hay que señalar que este algoritmo en el fondo no mejora exponencialmente los cálculos clásicos, ya que siempre se puede diseñar un algoritmo clásico probabilista (consultas aleatorias a la función) que nos dé el resultado con gran margen de precisión en muy poco tiempo.
Este algoritmo fue propuesto por Daniel Simon en 1994. Se trata de encontrar el periodo de una función vectorial booleana del tipo:
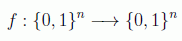
El periodo por tanto será un vector booleano T que cumpla:
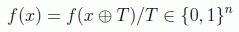
Se puede probar que de nuevo clásicamente habría que evaluar f sobre la mitad más uno de los elementos del dominio (2n-1+1), es decir, el coste sería exponencial. Incluso con un algoritmo probabilista no podríamos ir más acá de las 2n/2 consultas. Veremos que en este caso la ganancia cuántica es clara ya que bastará evaluar Uf unas pocas veces, del orden de n, para encontrar el periodo con una buena cota de aproximación.
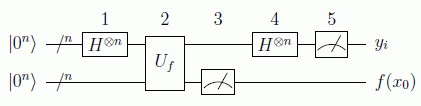
Ahora los dos registros del estado inicial tienen n qubits:

Aplicando los operadores de Hadamard al primer registro obtenemos:
Si hacemos actuar ahora la función obtenemos, dado que todos los bits del registro están a cero:
Ahora añadimos un paso que no es necesario pero sí es muy útil desde el punto de vista pedagógico. Se trata de medir el segundo registro y obtener uno de los posibles valores de la función, digamos f(x0), quedando el estado colapsado a:
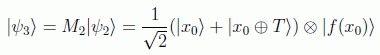
en donde por supuesto suponemos el estado más general combinación de x0 y x0+T, dado que sólo conocemos el valor de la función. Si ahora aplicamos Hadamard sobre los primeros qubits se obtiene:
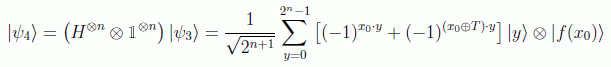
en donde lógicamente ahí sólo sobrevivirán los términos que cumplen que T· y=0, ya que el resto interferirá destructivamente. Si ahora medimos el primer registro:
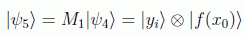
obtendremos para cada estado yi una probabilidad:
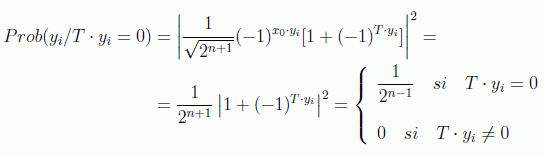
Repitiendo estos pasos del orden de n veces obtenemos n vectores yi que nos darán un sistema lineal homogéneo de ecuaciones cuya solución no trivial nos dará las componentes de T:
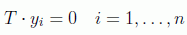
que podemos resolver con un algoritmo clásico obteniendo T con un orden O(n) de repeticiones. Como se ha dicho, este algoritmo es exponencialmente más eficiente que cualquier algoritmo clásico, incluso de tipo aleatorio.
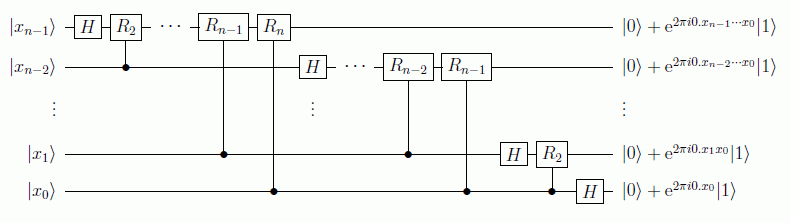
Hemos visto en los algoritmos estudiados que una de las armas más potentes en computación cuántica es la puerta de Hadamard. En realidad esta puerta es un caso especial de la llamada transformada cuántica de Fourier (QFT):
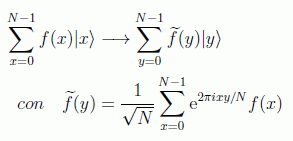
Por tanto, sobre los vectores de la base se aplica la transformación unitaria NxN:
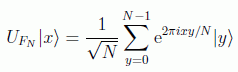
La QFT es por tanto una transformada de Fourier discreta (DFT). En principio harían falta del orden de O(N2) operaciones para realizarla, pero en el caso de N=2n, el orden O(22n) se puede reducir mediante la llamada transformada rápida de Fourier (FFT) a un orden de O(NlogN)=O(n2n). Aún así, sigue siendo un orden exponencial que veremos que el algoritmo cuántico mejora a cuadrático.
En este caso binario sustituiremos en la última expresión la expansión binaria:
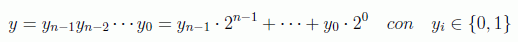
obteniendo
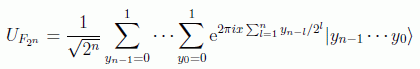
y utlizando que la exponencial de una suma es el producto de las exponenciales resulta:
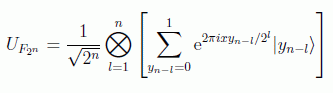
En consecuencia se puede ver que la QFT transforma la base computacional en otra base con vectores factorizables, es decir, sin entrelazamiento.
Ahora, teniendo en cuenta la representación de las fracciones binarias:
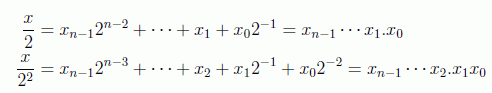
y despreciando la parte entera que en la exponencial sólo formará unidades, se tiene:
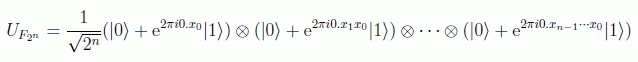
o de forma más compacta
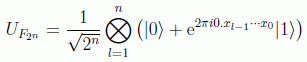
Nótese que como comentamos la puerta de Hadamard no deja de ser una transformada de Fourier actuando sobre un solo qubit:
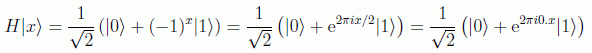
Vamos a ver un circuito que implementa esta transformación. Sea el caso n=3 con el estado de entrada:
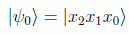
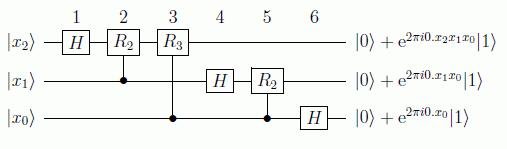
En donde definimos las rotaciones condicionales como:
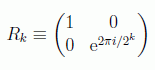
La primera puerta de Hadamard actúa sobre el bit más significativo, generando el estado:
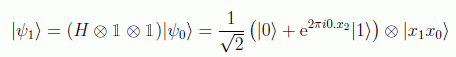
Las siguientes puertas de rotación controlada agregan las fases π/2 y π/4 a |x2> si los bits correspondientes están encendidos, esto es:
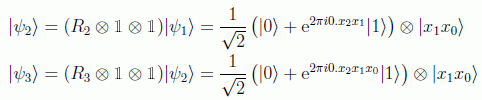
De la misma forma se aplica Hadamard y su rotación controlada al segundo bit:
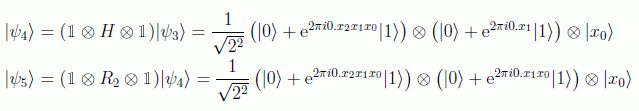
y por último la puerta de Hadamard al último bit:
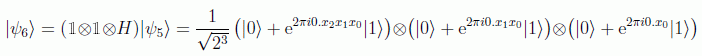
Vemos que para n=3 se han necesitado 3 puertas de Hadamard y 3 puertas de rotación condicionada. Para el caso general se necesitan:

Por tanto, el orden de cálculo de esta transformación cuántica es O(n2)=O((logN)2), lo que denota una ganancia exponencial frente al mejor algoritmo clásico, que como comentamos era del orden O(n2n).
Por claridad no hemos incluido las puertas SWAP que se necesitan (del orden de n/2) para obtener el orden correcto al final para nuestra transformada de Fourier tal como la definimos al principio. Un circuito general para n qubits sería de la forma:
Un algoritmo de búsqueda es el que nos permite encontrar un elemento x0 en un conjunto posible de soluciones (estructura de datos) que cumpla una determinada proposición f(x). Dentro de este tipo de problemas están la búsqueda en una base de datos o el coloreado ordenado de una gráfica.
Si no sabemos nada sobre la estructura del espacio de soluciones estamos ante un problema desestructurado, como el que resolvió Lov K. Grover en 1996. Un ejemplo sería la búsqueda de un teléfono en una guía telefónica sin conocer el nombre. Clásicamente el mejor algoritmo aleatorio nos llevaría a un coste de O(N) (si se quiere N/2 consultas de media) para una base de datos de tamaño N. Con el algoritmo de Grover se mejora este resultado con una ganancia cuadrática de orden O(√N). El algoritmo de Grover es probabilístico, es decir, sólo da la respuesta correcta con cierta probabilidad (al contrario que el de Deutsch por ejemplo que era determinista).
Lógicamente nuestra proposición aquí está implementada por un oráculo que actúe de la siguiente forma:
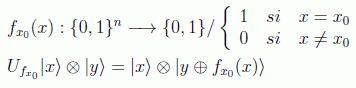
Por tanto, asumimos que de entrada necesitaremos un registro fuente de n qubits tal que N=2n y uno adicional para almacenar la información de la función. (Nótese el hecho de que conocer de antemano x0 no es lo mismo que reconocerlo entre un conjunto de estados).
La estrategia será preparar un estado superposición de todas las entradas del catálogo:
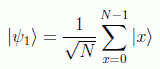
después aplicar el oráculo que nos dé todos los valores de la veracidad de la proposición sobre las entradas:
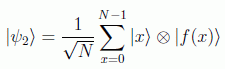
para en último lugar desbalancear los pesos estadísticos de forma que halla suficiente probabilidad de encontrar el estado |x0>|1>. Para ello hay que utlizar las operaciones de cambio de signo e inversión sobre el promedio.
Se trata de aplicar un cambio de signo al elemento que cumpla la proposición, de forma que quede de algún modo marcado (figura).

En el algoritmo clásico esto ya supondría, lógicamente, el haberlo encontrado, pero recordemos que aquí el elemento sigue dentro de un estado global que todavía no podremos medir por no tener la suficiente certeza de que el resultado nos va a dar nuestro elemento. El operador a implementar será de la forma:
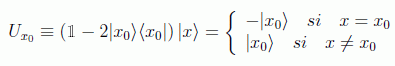
La forma de implementar este algoritmo es preparando un estado destino, tal como hicimos para el de Deutsch-Jozsa (inicializandolo a |1> y aplicando Hadamard), en |0> - |1>. De este modo el oráculo de la función nos dará un cambio de signo cuando ésta sea 1.
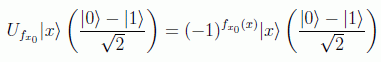
es decir, al no alterarse el segundo registro lo que se tiene es que:
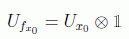
De esta forma el oráculo marca la solución del problema, mediante el operador cambio de signo:
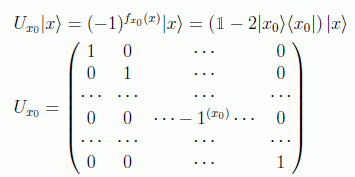
Para N=4 por ejemplo este operador oráculo se puede implementar mediante las siguientes puertas de tipo Toffoli, dependiendo de si el x0=0,1,2,3:
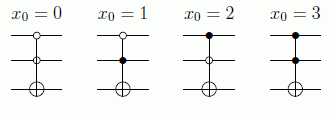
Se trata de un algoritmo que superpone sobre la media la diferencia respecto de ésta. De este modo el valor negativo recientemente invertido aparecerá por encima de todos los demás (figura). Para ello hay que usar el llamado por Grover operador de difusión:
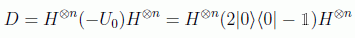
El efecto de este operador es equivalente a realizar una reflexión respecto del estado:
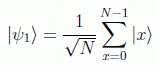
es decir
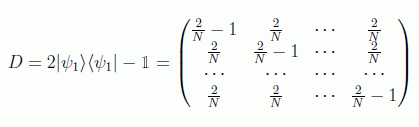
lo que se deduce simplemente aplicando la definición del operador Walsh-Hadamard respecto al estado fundamental y calculando después los elementos de matriz respecto de la base computacional.
Lo más interesante de este operador es estudiar lo que hace con las componentes de cualquier entrada que se le ponga, del tipo general:
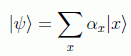
cuya acción es
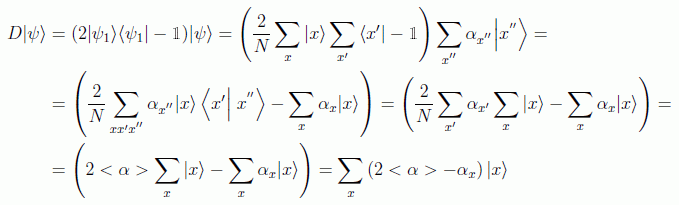
es decir, se produce un cambio de las amplitudes en la forma

Vamos a ver el ejemplo de la actuación del cambio de signo y esta inversión para el caso N=4 (que puede ser implementado con dos qubits). En el registro entrante las amplitudes de todos los estados son las mismas:
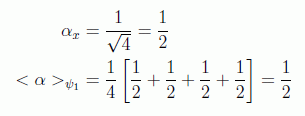
si se aplica un cambio de signo (sea x0=2=(10)):
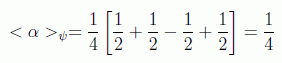
y por último aplicamos el operador de difusión, con lo que las amplitudes cambian a:
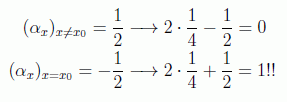
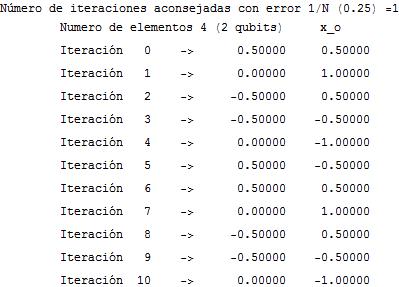
Lo que indica que en una sola iteración ya tenemos la certeza absoluta de encontrar el elemento, frente a una media de 2 en el caso clásico. En la figura anterior se ven las primeras iteraciones en este caso (y lo perjudicial que puede ser calcular de más). En general podemos decir que el aumento que se produce en la inversión temporal es aproximadamente:
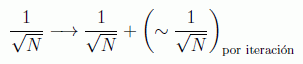
lo que sería una forma heurística de ver que en efecto el método de Grover es de orden O(√N), dado que con ese orden de iteraciones llegaríamos a la unidad. En realidad esto no es así dado que las sucesivas iteraciones no tienen el mismo comportamiento, por eso va a ser tan importante calcular el número de iteraciones suficiente para una cierta probabilidad.
Para implementar este algoritmo basta con saber cómo se implementa la inversión respecto del eje |0> dada por -U0. Para ello se usa el hecho de que:
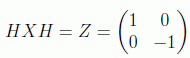
A partir de esto podemos construir, con ayuda de puertas CNOT o Toffoli controladas, el operador que actúa reflejando el último vector de la base |111···1>. Si nos ayudamos también de puertas X podemos dar la vuelta al estado de forma que lo que gire sea el primero. Por ejemplo, para dos qubits tendríamos:
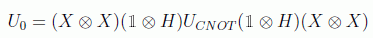
y el circuito correspondiente a U0 sería:
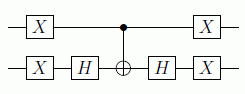
como para implementar una puerta de Toffoli de n bits se necesitan 2n-5 puertas ternarias de Toffoli, será ese el orden de cálculo de este algoritmo, es decir O(n)=O(log N).

Partimos de un estado entrante de la forma:
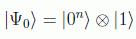
y al pasar por las puertas de Hadamard se tiene:
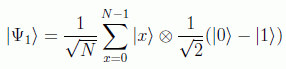
Como a partir de aquí el segundo registro no se va a modificar, es útil trabajar sólo con el primero y empezar con el estado:
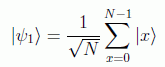
y estudiar su evolución bajo las iteraciones del operador de Grover:
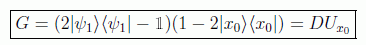
y de esta forma también podemos simplificar su representación gráfica:
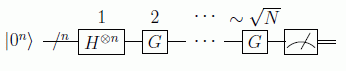
donde
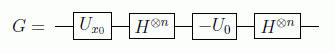
Por tanto la primera reflexión respecto a |x0> nos dará en el primer registro el resultado:
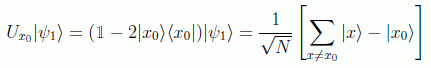
y la inversión sobre el promedio nos da:
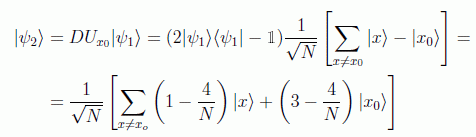
en donde se ve claramente que para N=4 con una sola iteración ya se puede medir. Si continuamos el siguiente paso nos daría:
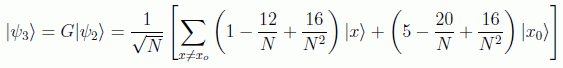
La expresión general es difícil de compactar con fracciones polinómicas (seguramente habría que hacer uso de las funciones de Chebyshev), pero tiene una expresión trigonométrica particularmente sencilla:
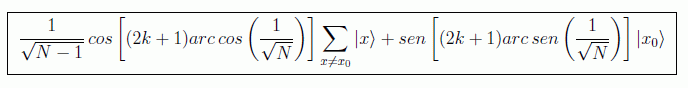
El estado |ψ1 se puede separar mediante una base reducida en dos estados ortonormales:
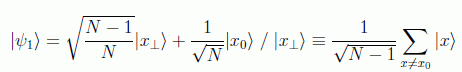
De forma que Ux0 es una simetría respecto a |x⊥> y D es una simetría respecto a |ψ1> que en este caso tiene la forma:
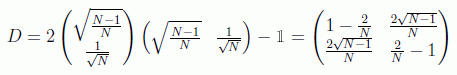
Por geometría básica se sabe que la composición de dos reflexiones de ejes secantes es un giro de ángulo doble al que forman los ejes. Sea ese ángulo de giro θ, luego el que forman los ejes será la mitad y
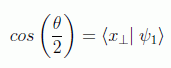
luego
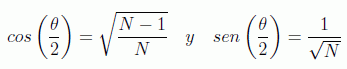
Si llamamos γ=θ/2 el estado inicial es
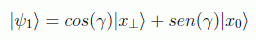
y la aplicación del algoritmo supone un giro de θ=2γ en ese plano, es decir
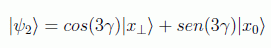
por lo que después de k interacciones tendremos
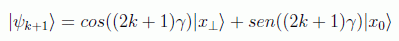
Es obvio que para rotar completamente el estado |ψi> a |x0> se debe cumplir:
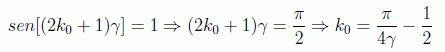
Expresión que no es entera, y por tanto habrá que aproximar, y aquí es cuando sale la dependencia del algoritmo en cuanto al orden O(N).
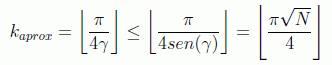
Vamos a calcular la probabilidad de fallo, definida como
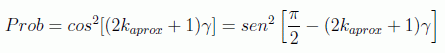
usando el siguiente hecho
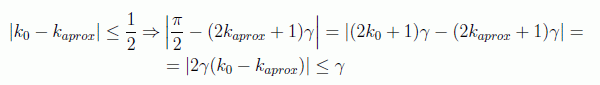
por tanto
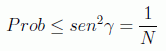

Y por esto la probabilidad de fallo después de π√N/4 iteraciones es 1/N. Normalmente además la probabilidad de encontrar el elemento es mayor que esta cota, como se aprecia en la figura anterior para 64 elementos, en donde aunque esta probabilidad es de 0.016, en realidad en la iteración recomendada tenemos una amplitud de 0.998, con lo que el margen de error probabilístico es de 0.004.
Para introducir la dependencia con el número de soluciones hay que definir los conjuntos:
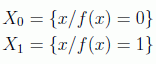
de forma que, si s es el número de soluciones
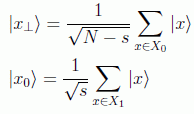
y por tanto
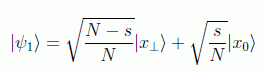
Y de nuevo tendremos la misma interpretación trigonométrica:
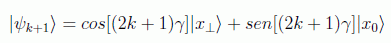
solo que ahora el ángulo se define como
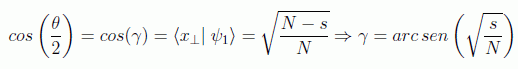
Así que por la misma razón ahora el orden de iteraciones va con O(√N/s):
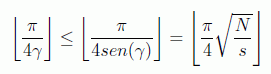
con una probabilidad de error de s/N.
Casos particulares interesantes son:
s=1. Ya hemos visto que si N es grande:
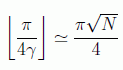
s=N/4. En este caso sen(γ)=1/2 y
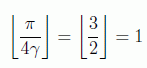
es decir, con una sola iteración se consigue la solución.
s=N/2. Entonces sen(γ)=1/√2 luego γ=π/4 y
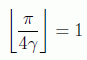
pero en este caso la aplicación del algoritmo no mejora la probabilidad de acierto clásica, que sigue siendo s/N=1/2:
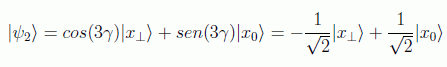
s>N/2. A partir de aquí, el número de iteraciones se va haciendo más grande y no se gana respecto al caso clásico, ya que el ángulo de giro cumple:
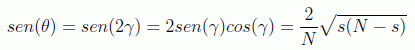
expresión que alcanza su valor máximo en s=N/2, con lo que después desciende y por tanto el número de iteraciones será mayor.
De todo esto se deduce que si a priori no se conoce el número de soluciones el algoritmo no es útil. En efecto, si por ejemplo N=220, ya hemos visto que una probabilidad de fallo menor que 2-20 nos la darían, para una solución
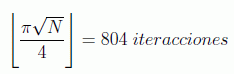
pero si mantenemos este número de iteraciones y resulta que existen s=4 soluciones el error que se comete es muy grande, ya que en este caso deberíamos haber empleado 402 iteraciones, encontrando para el valor 804:
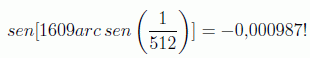
cuando teníamos que haber parado en el 402:
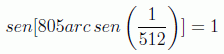
No obstante, hay formas de usar el algoritmo de Grover más cuidadosamente cuando uno tiene pistas sobre el número de soluciones (Boyer, Brassard, Hoyer, Tapp, 1996), e incluso un algoritmo de conteo de soluciones mediante la transformada de Fourier (Brassard, Hoyer, Tapp, 1998).
Para hallar la relación de recurrencia escribimos el estado en la forma:
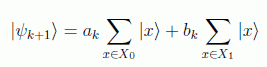
en donde la semilla es
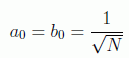
Como en cada iteracción las amplitudes cambian de signo y se produce la inversión en el promedio, las relaciones recursivas son
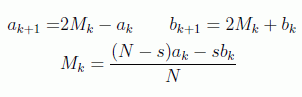
En forma matricial
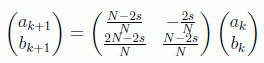
Por inducción se puede demostrar que la solución de este sistema es precisamente el resultado obtenido geométricamente:
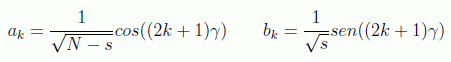
Un artículo de los profesores Galindo y Martín-Delgado de la Universidad Complutense aparecido en Physical Review en el 2000, titulado "Family of Grover's quantum-searching algorithm" abrió varias vías de investigación sobre los algoritmos de tipo Grover.
La más evidente es la posible generalización aprovechando el hecho de que (véase la transformada cuántica de Fourier)
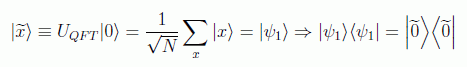
por tanto la inversión sobre la media toma la misma forma matricial en la base de momentos que el cambio de signo en la de coordenadas. Si definimos
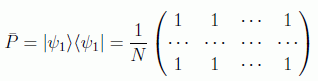
en la base transformada toma la forma:
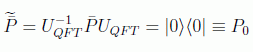
Esto, aparte de abrir el estudio hamiltoniano del sistema que ya se había dado (Farhi, Gutmann, 1998), nos puede inducir a descubrir qué pasaría si se utiliza un proyector sobre otro estado de "momento". Los estudios hechos muestran que el caso concreto encierra toda la esencia del algoritmo, parece que no aportando la generalización nuevos hechos.
En cualquier caso, el artículo aludido se centra en la generalización de los operadores de Grover a operadores de la forma:
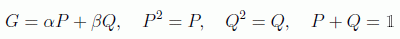
definiendo la iteración de Grover como la composición de dos de estas superposiciones de proyectores ortogonales, con el llamado kernel de Grover:
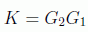
donde
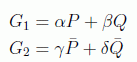
con
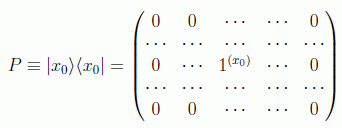
La elección particular de Grover lógicamente es
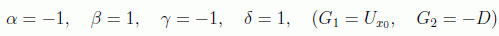
en general podemos poner
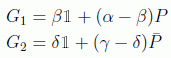
que en forma matricial en la base reducida ya estudiada
toma la forma
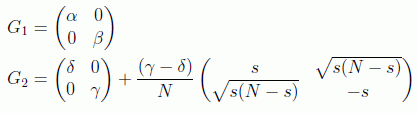
Pero lógicamente en el kernel cada operador de Grover tendrá una libertad de fase con la que podemos reducir a dos el número de grados de libertad, fijando por conveniencia:
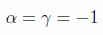
con lo que un cálculo fácil nos da la expresión para el kernel en la base reducida:
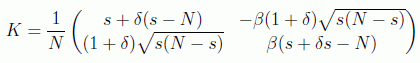
La estrategia de generalización se basa en recoger la expresión para la amplitud de probabilidad después de m iteraciones del kernel:
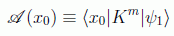
entonces, si somos capaces de diagonalizar K en términos de sus autovectores {|k1>,|k2>} y autovalores { eiω1,eiω2} la expresión quedaría más manejable y podríamos sacar conclusiones.
El caso s=1 estudiado en el artículo nos daría un desarrollo:
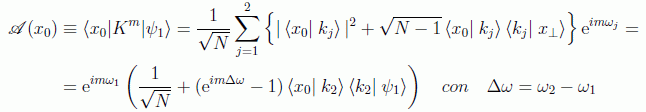
un estudio para N⟶∞ de estos autovectores nos da
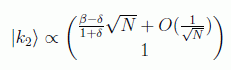
pero el primer sumando de la primera componente nos daría una probabilidad no convergente, con lo que necesariamente
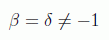
y de este modo se obtiene
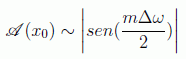
que alcanza su valor máximo en
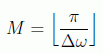
y teniendo en cuenta que la expresión de los autovalores da un comportamiento asintótico cuando N⟶∞ de
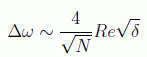
si parametrizamos el parámetro de Grover como δ= eiΦ se tiene la expresión
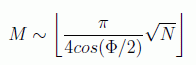
obteniendo por fin una expresión generalizada para la eficacia de los algoritmos tipo Grover. Lógicamente para Φ=0 recuperamos el principal. Además en el artículo mencionado se hace un estudio de las perturbaciones sobre las condiciones iniciales viendo su estabilidad.