
RELATIVIDAD RESTRINGIDA

Los orígenes de la Relatividad Restringida, también llamada Relatividad Especial, se hallan en los éxitos conseguidos por la teoría electromagnética de Maxwell en el siglo XIX.
Los experimentos diseñados para hallar la velocidad de la luz en el vacío que surgía de las ecuaciones de onda de Maxwell para el campo electromagnético, parecían indicar que ésta era siempre la misma independientemente del estado de movimiento del emisor. Estos hechos, unidos a la desestimación experimental del llamado "éter luminífero", condujeron a los físicos a pensar lo inevitable: la incorrección de la mecánica newtoniana establecida dos siglos atrás.
Como es costumbre en la historia de la ciencia, primero se intentaron hacer algunas mejorías adicionales pequeñas, y los primeros intentos se deben al irlandés G.F. Fitzgerald y al holandés H.A. Lorentz en 1892. Pero fue Albert Einstein el que en 1905, su conocido ''annus mirabilis" (''año milagroso"), resolvió el problema mediante una revisión profunda de los conceptos de espacio, tiempo y energía en su famoso artículo "Zur Elektrodynamik bewegner Körper" ("Sobre la electrodinámica de los cuerpos en movimiento") en el número 17 de la revista alemana Annalen der Physik.
En aquel momento lógicamente nadie había tenido ningún problema al hablar de conceptos como la velocidad del sonido al relacionarlos con la ley de adición de velocidades de Galileo (relatividad galileana). El sonido siempre se propaga con una velocidad relativa al aire, y las propiedades de éste pueden ser estudiadas, además de por la propagación del sonido, por los más diversos métodos físicos y químicos de investigación. Es decir, en general, cuando decimos que la velocidad del sonido tiene un cierto valor, sabemos que en realidad medimos la velocidad de una onda con relación al medio en el que se propaga. El sonido no se propaga en el vacío.
Sin embargo, ¿qué ocurre con la velocidad de la luz? Las ecuaciones de Maxwell le confieren un valor determinado, de c=300.000 km/s aproximadamente, en cuanto a su propagación en el vacío. Sin embargo, la relatividad galileana exige un sistema de referencia en reposo respecto del cual podamos definir esa velocidad de propagación, y para todos los sistemas móviles respecto a él habría que aplicar las conocidas transformaciones de Galileo. Por ejemplo, las coordenadas y los tiempos que se deben medir en un sistema móvil (x',y',z',t') que se mueve alejándose en la dirección x con velocidad constante v respecto de un sistema en reposo (x,y,z,t) serían:
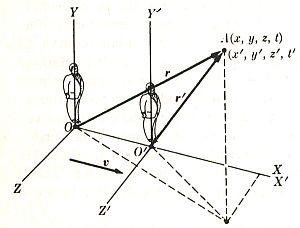
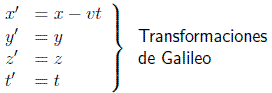
Parecía entonces urgente encontrar ese sistema de reposo absoluto respecto al vacío en donde estaban bien definidas las ecuaciones de Maxwell. En este laboratorio la luz se propagaría en todas direcciones con igual velocidad c, y en cualquier otro laboratorio debería haber desviaciones. Es por esto que los físicos, tomando prestado un término aristotélico, introdujeron el concepto del éter como el sustrato cuyas vibraciones se manifestaban en forma de luz y por el que todos los cuerpos se podían mover libremente. Sería este el sistema de reposo absoluto respecto al vacío.
Sin embargo, la hipótesis del éter parecía ser bastante arbitraria y provocaba más de un interrogante. Parecía no intervenir en ningún proceso físico y ser absolutamente indetectable. Además, no debería infligir a los cuerpos ninguna clase de rozamiento. Los físicos ya antes habían tenido experiencias infructuosas al introducir el flogisto y el calórico para explicar las combustiones y algunos fenómenos térmicos.
Aunque algunos físicos ya intuían la futilidad de este concepto, se hacía necesario diseñar algún experimento para confirmarlo o deshecharlo.
El primero en realizar un experimento que confirmara la teoría del éter fue el físico americano de origen polaco Albert Abraham Michelson en 1881. Lo que se pretendía medir era la diferencia entre los recorridos de la luz dependiendo de su dirección respecto a un laboratorio móvil respecto al éter. ¿Y qué mejor laboratorio móvil que nuestro propio planeta? Además con una velocidad bastante importante, de unos 30 km/s en su órbita alrededor del Sol (prescindimos del movimiento de rotación que tiene una velocidad de medio kilómetro por segundo aproximadamente).
Por tanto, considerando pues que la Tierra se mueve con una velocidad v respecto al éter de forma rectílínea (en la ínfima parte de un segundo que requerirá nuestro experimento, se puede decir que la Tierra se mueve respecto al éter con movimiento rectilíneo uniforme), el recorrido que hará la luz en ir desde una fuente luminosa situada a la izquierda hasta un espejo en la derecha a una longitud L de distancia y volver, siempre en la dirección de v, será:
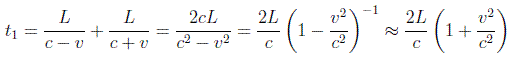
Al principio físicos como Maxwell pensaban que esta desviación del orden de v2/c2=10-8 no se podría medir experimentalmente, sin embargo Michelson empezó a pensar en un método que le permitiese conseguirlo. Y en 1881 diseñó su primer experimento, con el interferómetro que se muestra en la figura:
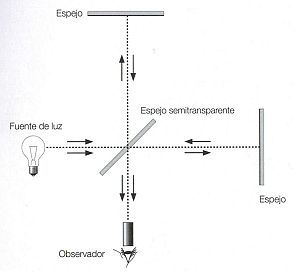
La luz procedente de una fuente incide sobre una lámina de cristal inclinada que posee una capa de cristal semitransparente en su cara anterior y está situada a una distancia L de dos espejos. Esta lámina divide a la luz en dos partes. Una la atraviesa y llega al espejo de la derecha y a la vuelta se refleja y llega al observador (telescopio). La otra va por reflexión al espejo de arriba y vuelve atravesándola otra vez hasta el observador, pasando antes por una lámina de compensación para conseguir la simetría óptica (que los dos haces pasen por el mismo espesor de cristal).
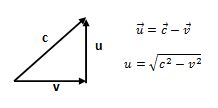
En cuanto al haz vertical, aplicando cálculo vectorial básico tendrá una velocidad respecto al éter de u=c-v. por tanto el tiempo que emplea este haz será por su parte:
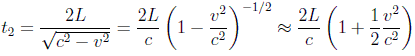
y por tanto la diferencia de tiempos de los dos rayos será:
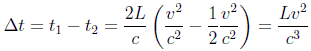
Esta diferencia de tiempos ha de detectarse observando la interferencia de los dos haces de luz. Debido a la dificultad que supone conseguir que los dos trayectos sean de la misma longitud con la precisión requerida, se observa el diagrama interferencial de los dos haces y luego se hace girar el aparato completo 90º. La rotación produce una diferencia de tiempos como la anterior para cada haz. La diferencia de tiempo total de 2Δ t es equivalente a una diferencia de trayectos de 2cΔ t. Las franjas de interferencia observadas en la primera orientación deberán así desplazarse en un número de franjas δ dado por:
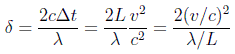
en donde λ es la longitud de onda de la luz utilizada. Los valores de L y c también son conocidos, pero, ¿qué valor deberemos dar a v? Ya hemos dicho que se había aceptado para ello la velocidad de la Tierra en su órbita, de unos 30 km/s, lo que hacía que v/c aprox. 10-4. En el primer intento de Michelson en 1881 los demás valores eran λ aprox. 6 x 10-7 m y L=1,2 m, se tiene que λ/L aprox. 5 x 10-7. Por tanto el corrimiento debía ser de δ aprox. 0,04 franjas. Este efecto es muy pequeño, pero podría haberse observado de no ser que, para sorpresa de Michelson, no hubo ningún corrimiento de franjas. En la presentación de su resultado se puede leer: "El resultado de la hipótesis de la existencia de un éter estacionario demuestra, por tanto, que es incorrecto".
Este resultado era tan inesperado y tan difícil de explicar que condujo a renovados esfuerzos, en especial por parte del gran físico holandés H.A. Lorentz, quien para reconciliarlo con otros fenómenos ópticos propuso una teoría de acuerdo con la cual podría existir un arrastre parcial del éter por parte de la Tierra. Era oportuna una repetición más precisa del experimento y Lord Rayleigh escribió a Michelson urgiéndole a que la realizara. Así fue cómo Michelson, ahora en colaboración con E. W. Morley, emprendió una investigación mucho más precisa, basada en caminos ópticos unas 10 veces más largos que en el primer experimento. El corrimiento esperado ahora era de unas 0,4 franjas, pero en los resultados obtenidos se observó un corrimiento de unas 0,005 franjas a lo sumo. Esta versión refinada del experimento, llevada a cabo en 1887, es considerada como uno de los pilares experimentales básicos sobre los que descansa la Relatividad Especial.
A pesar del resultado del experimento de Michelson, los físicos se aferraban a la idea del éter, un sistema de referencia en reposo absoluto. El irlandés G.F.Fitzgerald y el holandés H.A. Lorentz independientemente propusieron la idea de que lo que se producía era una contracción real de la longitud de los cuerpos según la dirección en que se mueven a través del éter, y además esa contracción en la dirección de la velocidad tendría que valer exactamente (1-v2/c2)1/2 para explicar el hecho de que el corrimiento de franjas era nulo.
No obstante, se podía intuir que esto era una explicación ad hoc un poco forzada. Fue Einstein el que pudo dar una explicación natural retomando un principio clásico de la Física, el principio de relatividad de Galileo:
Todas las leyes de la Dinámica deben ser las mismas para todos los observadores inerciales, moviéndose con velocidad constante unos con respecto a otros.
Einstein sabía que este principio era sobre el que debía descansar la Física, por su belleza y simpleza. Y quería extenderlo a los nuevos fenómenos físicos descubiertos en Óptica. Empezó a imaginarse qué ocurriría si se viajara en un rayo de luz a velocidad constante y supusiéramos que el viajero debería ver la misma física que el observador en reposo. Y fue entonces cuando se dio cuenta de que si se aceptaban las transformaciones de velocidad de Galileo aquello no podía funcionar. El viajero en la luz debería ver un campo electromagnético estático, cosa que no existía en la teoría electromagnética. La luz por tanto debería seguir moviéndose a la velocidad descrita por las ecuaciones de Maxwell. Esto fue lo que le condujo a enunciar su principio de relatividad, añadiendo la constancia de la velocidad de la luz.
1) La velocidad de la luz en el espacio libre, c, es una constante de la Naturaleza, independiente del estado de movimiento de la fuente.
2) Todas las leyes de la Naturaleza (no solamente de la Dinámica) deben ser las mismas para todos los observadores inerciales moviéndose con velocidad constante unos con respecto a otros.
Una vez así aceptada como ley natural la constancia de la velocidad de la luz, el principio de relatividad restringida reafirmaba las leyes del electromagnetismo. Pero el precio a pagar era, sin embargo, una revisión de la mecánica newtoniana que haría cambiar dramáticamente nuestra concepción del espacio y, sobretodo, del tiempo.
Una vez admitidos estos postulados, Einstein se dio cuenta de sus implicaciones. Una de las más asombrosas era que el concepto de simultaneidad dejaba de tener sentido, o al menos sólo lo tenía cuando se comparaban dos relojes en reposo. El tiempo era, pues, relativo.
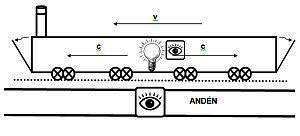
En efecto, imaginemos un tren que se mueve a velocidad constante en cuyo vagón central hay una fuente de luz, y supongamos que en el primer y último vagón hay instaladas unas puertas que se abren al recibir esa luz. Lógicamente, para un observador situado en el centro del tren las dos puertas se abrirán simultáneamente. Pero, qué es lo que verá un observador situado en el andén si la fuente se enciende a su paso? Recordemos que la velocidad de la luz respecto a él tiene exactamente el mismo valor que respecto al viajero. De aquí se deduce que, dado que las traseras del tren van al encuentro del rayo de luz, este observador verá la puerta trasera abrirse antes que la delantera y, por tanto, para él los sucesos no serán simultáneos.
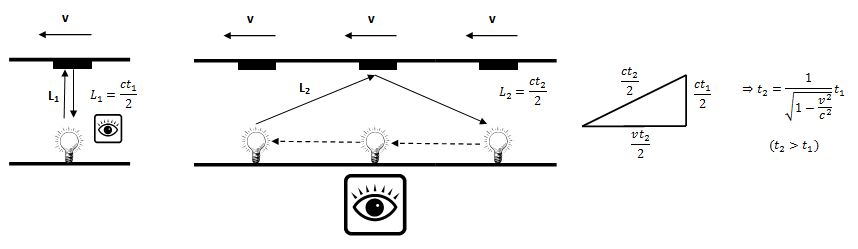
Todavía, no obstante, se pueden obtener consecuencias más chocantes. si imaginamos que el mismo pasajero del vagón tiene una linterna que apunta a un espejo en el techo, la trayectoria de la luz para él será una línea vertical hacia arriba y de vuelta hacia abajo y si usa un cronómetro muy preciso, el tiempo que mide será t1=L1/c. Sin embargo, para el observador del andén, la trayectoria de la luz, al estar el tren en movimiento, será mayor, L2>L1, consistirá en dos líneas oblicuas de ida y vuelta, y por tanto medirá un tiempo mayor, t2=L2/c. De lo que se deduce que, si estos dos observadores se citan un día podrán constatar que para el que estuvo en movimiento pasó menos tiempo que para el que estuvo en reposo. ¡Los relojes en movimiento se atrasan inevitablemente!
Para clarificar los conceptos asociados a la Relatividad Especial fueron de mucha utilidad los gráficos introducidos en 1908 por el matemático alemán Hermann Minkowski. Según este sistema, si llamamos A y C a los puntos extremos del primer tren y B donde se ubica la fuente de luz, tendremos definida una "superficie" de simultaneidad como A1C1, que para el caso de un tren en reposo será como en la figura:
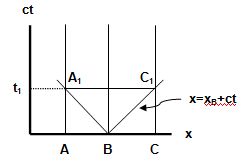
Obsérvese que las llamadas líneas de universo de un objeto en reposo son rectas verticales y las de un rayo de luz son paralelas a las bisectrices de los ejes. Para el caso en que A, B y C estén en movimiento, las líneas de A y C estarán ahora inclinadas y los sucesos no serán simultáneos en el sistema en reposo:
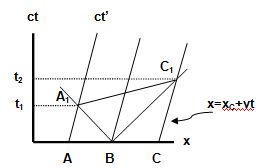
Hay que tener en cuenta que estos diagramas se han hecho bidimensionales por comodidad, pero en realidad tendríamos siempre tres dimensiones espaciales y la temporal. Para un suceso dado P podemos dar sus coordenadas en cualquiera de los sistemas inerciales mediante las líneas oblicuas anteriormente explicadas. En la figura siguiente tenemos el caso de dos sistemas de coordenadas superpuestos, uno con velocidad v respecto al otro:
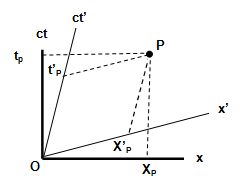
Vamos a buscar las relaciones entre los diferentes sistemas inerciales. Si suponemos que cuando los dos sistemas coinciden se emite un rayo de luz, para ambos sistemas este rayo tendrá la ecuación de la bisectriz x=ct o x'=ct'.
Para el observador en reposo, el origen del sistema de coordenadas en movimiento se ve lógicamente con la trayectoria OO'=vt, luego lo que buscamos serán unas transformaciones simétricas de la forma:
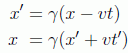
de forma que si x'=0 el desplazamiento sea el del origen x=vt. Si sustituimos la expresión del rayo luminoso y eliminamos las dos variables temporales:
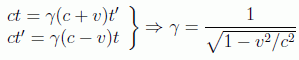
Y una vez obtenidas estas ecuaciones podemos deducir también las relaciones para los tiempos:
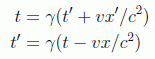
Y podemos ya escribir las transformaciones de Lorentz de la Relatividad Restringida:

llamados así debido a que el primero en introducirlas fue Lorentz en 1904 para explicar el resultado del experimento de Michelson, aunque fue Albert Einstein el que les dio su verdadero significado.
Es fácil comprobar que estas transformaciones son las de Galileo a bajas velocidades y que definen el llamado invariante espacio-tiempo:
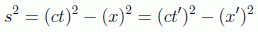
en donde por comodidad hemos vuelto al caso unidimensional. Este invariante nos proporciona un método para "calibrar" los diagramas de Minkowsky, como se muestra en la figura siguiente, de forma que la hipérbola rectangular:
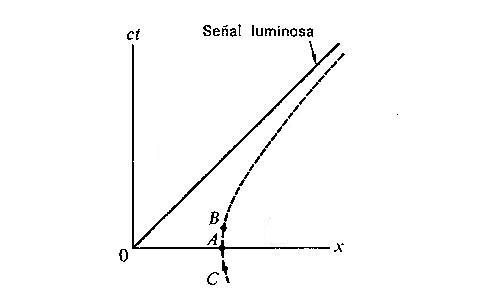
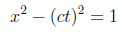
nos definirá una distancia unidad para todos los ejes inerciales, es decir, es el lugar geométrico en el espacio-tiempo de todos los sucesos que representan el tiempo cero y la coordenada x igual a la unidad en sistemas inerciales diferentes.
Obsérvese que en este último caso s2=-1, ¿cómo se puede interpretar este invariante? Podemos denominarlo intervalo entre dos sucesos en el espacio-tiempo; se hace nulo para aquellos sucesos conectados mediante una señal luminosa, se dice que están conectados por una líneas de luz (rayo de luz), que en los diagramas de Minkowsky se representan por las rectas x=± ct, que en dimensión 2+1 define lo que se conoce como cono de luz:
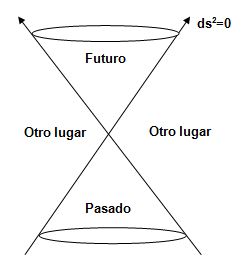
Si s2>0 se habla de intervalo de género tiempo, son sucesos que acontecen en el mismo lugar para algún sistema inercial, de forma que entre ellos se puede establecer una relación de causalidad. Si s2<0 se habla de intervalo de género espacio, en donde siempre habrá una transformación Lorentz que nos lleve a un inercial en el que estos sucesos sean simultáneos, con lo que no estarán conectados por ninguna relación causal por necesitarse una velocidad de transmisión superior a la de la luz.