
INTRODUCCIÓN A LA COSMOLOGÍA

"La Cosmología es la ciencia que estudia el origen y la evolución del Universo como un todo". Esta definición o alguna parecida son las que se pueden encontrar en las enciclopedias, pero de hecho tienen su lado discutible. A mi juicio una definición más realista sería la que denota su significado etimológico: "discurso sobre el Cosmos", ya que en realidad en más de una ocasión esta materia ha estado alejada del método científico tal y como lo conocemos desde el Renacimiento.

En efecto, tanto en sus inicios con las teorías griegas como en épocas más recientes, el desarrollo de la Cosmología no ha ido de la mano de la observación experimental, por ser esta en general muy difícil de realizar, y sólo se utilizan ciertos hechos empíricos para dar argumentos de plausibilidad a tal o cual teoría imposible de comprobar experimentalmente hasta sus últimos términos. En la actualidad el experimento, especialmente las sondas enviadas al espacio y las radiaciones que del cosmos medimos en la Tierra, están impulsando una época dorada en la teoría cosmológica, y de nuevo los hechos nos sobrepasan. Pero todos somos conscientes de la parte especulativa que inevitablemente está asociada a esta rama de la Física. Pero hagamos un breve repaso.
Podemos situar el comienzo de la cosmología occidental hace 2500 años, en época griega. La primera gran teoría cosmológica, que perduró hasta el Renacimiento, fue la defendida por Platón y, sobre todo, Aristóteles, con sus cuatro elementos: tierra, agua, aire y fuego; y el movimiento eterno y perfecto de los objetos celestes fijados en ocho esferas cristalinas rotantes, cuya materia era la llamada quinta esencia. Todo impulsado por un Gran Hacedor, con la Tierra, por supuesto, en el centro.
La longevidad de esta cosmología aristotélica también se puede explicar por las modificaciones ad hoc que hizo el astrónomo Claudio Ptolomeo para explicar las obvias anomalías que se observaban en el movimiento de los astros (en especial la retrogradación de los planetas).
No fue hasta el año 1543 cuando el modelo geocéntrico de Aristóteles fue cambiado por el heliocéntrico del matemático polaco Nicolás Copérnico, que precisamente el año de su fallecimiento publicó su trabajo Sobre la revolución de las esferas celestes. Estas ideas se fueron aceptando gradualmente y perfeccionando por astrónomos como el alemán Johannes Kepler hasta el nuevo Universo gravitacional del inglés Isaac Newton, que perduró hasta que en el siglo XX Albert Einstein enunciara su teoría de la Relatividad General. En la última época de la Cosmología el discurso ha sufrido un cambio importante: el conocimiento del Universo a gran escala no podía separarse del estudio de la física de lo más pequeño, era inevitable que la Astronomía y la Física de Partículas fueran de la mano para elaborar cualquier teoría cosmológica.
Pero veamos brevemente algunas de las efemérides de la época moderna de la Cosmología:
Resumiendo, la Cosmología contemporánea se basa en tres grandes pilares: el principio cosmológico, la teoría del Big Bang y el paradigma inflacionario. Actualmente se admite que vivimos en un universo plano de unos 13.700 millones de años de edad que está en expansión, actualmente acelerada, y que posee unas anisotropías en el fondo de radiación, consecuencia de fluctuaciones cuánticas en el periodo de inflación, que originaron las galaxias por colapsos gravitacionales. Asimismo se ha deducido que sólo el 4,5% de la materia-energía del universo es bariónica, siendo el resto de la materia sólo el 22,5% del total, la materia oscura desconocida, de la que conocemos sólo sus efectos gravitacionales; y el resto, el 73% sería una energía oscura no detectada y de la que sólo conocemos sus efectos aceleradores. El modelo cosmológico más defendido actualmente es el modelo Lambda-CDM (Lambda-Cold Dark Matter).
El estudio del Universo requiere ciertas suposiciones que a veces son lamentablemente olvidadas. La primera por supuesto es que lo suponemos comprensible con la Física que elaboramos en nuestros laboratorios terrestres, es decir, se espera que las leyes físicas dentro del Sistema Solar sean aplicables al Universo entero a escala cosmológica, que las constantes físicas sigan siendo constantes, etc.
Una de las suposiciones más importantes es el llamado principio cosmológico, que afirma que todos los observadores fundamentales ven la misma cosmohistoria. Aunque veremos con detalle qué significan estos conceptos, adelantar que por observador fundamental se entiende aquel que habita en una galaxia promedio. En cierta medida este principio es opuesto a los llamados principios antrópicos, en donde nuestra posición en el Universo sería privilegiada.
Una de las consecuencias directas del principio cosmológico es suponer la homogeneidad e isotropía del Universo a gran escala. Hay indicios observacionales considerables de que la estructura del Universo presenta una extraordinaria uniformidad de materia y radiación en escalas de 108 años luz (al), es decir, unos cuantos cientos de millones de años luz (las galaxias típicas tienen cientos de miles de años luz de diámetro, 105). Cuando decimos uniformidad hablamos principalmente de densidad, presión y temperatura. Es obvio que en condiciones terrestres la materia no es homogénea e isótropa, sin embargo si tomamos como unidad el parsec (pc), la unidad astronómica equivalente a 3·106 m, poco más de 3 años luz, la cosa se ve mucho más homogénea. Actualmente la escala de homogeneidad e isotropía que se acepta es de 200 Mpc:
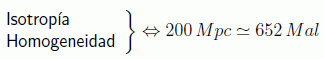
Así, si promediamos la densidad del Universo dentro de un cubo de arista 200 Mpc y trasladamos ese cubo una distancia mayor, la densidad media en el primer lugar será casi igual a la del segundo lugar.
El principio cosmológico también predice la geometría que debemos aplicar para medir distancias e intervalos temporales en esta escala, y para ello debemos encontrar la métrica que rige esta geometría a gran escala. Estos cálculos se basan por supuesto en la Relatividad General de Einstein, pero no hay que olvidar que todo se funda a su vez en los trabajos de los grandes geómetras, y aparte de los del padre de la geometría, Euclides, los trabajos de las geometrías no euclideas de los alemanes Carl Friedrich Gauss y Bernhard Riemann, el húngaro János Bolyai y el ruso Nikolái Lobachevski, en el siglo XIX, fueron determinates. Veamos pues cómo se deduce la métrica.
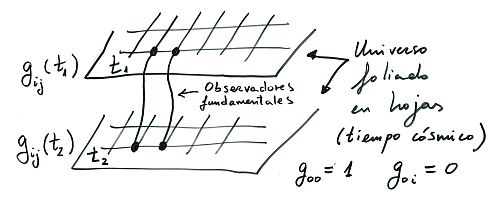
Normalmente se parte del llamado postulado de Weyl que asume la uniformidad del Universo como un sustrato o fluido perfecto en el cual las geodésicas son ortogonales a una familia de hipersuperficies de género espacio. Dicho de otra forma, se trabajará con lo que se conoce como coordenadas comóviles, que se definen por medio de las caídas libres de los observadores fundamentales, de forma que dos geodésicas no se intersecan excepto en algún punto singular del pasado o del futuro. Si los observadores fundamentales sincronizan sus relojes cuando para todos ellos los parámetros cosmológicos tienen los mismos valores (temperatura, presión, densidad media, etc) el tiempo común resultante es lo que se conoce como tiempo cósmico t, que definirá las superficies de simultaneidad. Los apuntes de los parámetros vistos por los observadores fundamentales es lo que llamamos cosmohistoria.
Hay muchas forma de llegar a la métrica con la simetría que buscamos, vamos a escoger aquí el camino rápido suponiendo ciertos conocimientos de Relatividad General. Para empezar admitiendo la isotropía del problema lo que estamos buscando es un invariante de la forma:
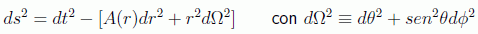
ya que el postulado de Weyl nos asegura que no haya términos cruzados y la homogeneidad nos permite olvidarnos de la dependencia temporal y trabajar sin ella de momento en una de las hipersuperficies u hojas en las que dividimos el espacio-tiempo. También la homogeneidad nos prescribe que el escalar de curvatura de Ricci debe ser constante en todo punto. Vamos a suponer para simplificar los cálculos que existen sólo dos dimensiones espaciales, con lo que tenemos los siguientes valores no nulos para la métrica:

que nos dará, recordando la definición de conexión afín, los siguientes símbolos de Christoffel no nulos:
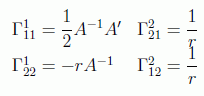
que nos dejan los siguientes valores para los elementos diagonales del tensor de Ricci:
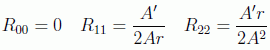
Todos estos cálculos se hacen con un sencillo programa en cualquier software matematico (aquí estan hechos con Mathematica). Sólo queda calcular el escalar de curvatura con nuestra métrica obteniendo una ecuación diferencial fácil de resolver:
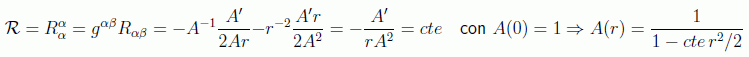
en donde hemos impuesto la condición inicial de que para entornos pequeños el espacio sea plano. Ahora sólo queda hacer la reescala:
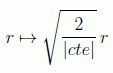
obteniendo la llamada métrica FLRW (Friedman-Lemaitre-Robertson-Walker), más conocida como métrica Robertson-Walker:
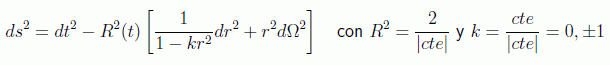
En donde se ha introducido el índice de curvatura k y el llamado factor de escala R(t), con dimensiones de longitud (r es adimensional en el modelo), ya con la dependencia temporal, que nos dará una información valiosa sobre nuestro universo. Nótese que la curvatura constante en el caso simplificado estudiado está dada por 2k/R2.

En el caso de 3+1 dimensiones se pueden concluir las mismas expresiones. En este caso las coordenadas (t,r,θ,φ) se llaman comóviles debido a que dos objetos permanecen en esas coordenadas todo el tiempo mientras lo que cambia es la distancia entre ellos de acuerdo al factor de escala R(t). El conocimiento de R(t) y, por supuesto, de k, es objeto de observación experimental e interpretación teórica por medio de las ecuaciones de la Relarividad General.
A menudo se suele ver la métrica de Robertson-Walker en la forma más compacta:
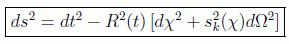
denominada representación comóvil, en donde la distancia propia es siempre proporcional a la coordenada radial comóvil, definiendo esta χ de forma que:

Como se puede ver, el caso del índice de curvatura positivo k=+1 es el único que nos da un espacio-tiempo cerrado, siendo los otros dos casos abiertos. Las topologías que aquí se muestran son las triviales, pero otro tipo de topologías también son posibles identificando puntos e intervalos. Asimismo hay otras formas de la métrica Robertson-Walker, como la conforme, en donde se reescala el tiempo para que juegue el mismo papel que el espacio, o la isótropa, en donde se utiliza la curvatura gaussiana del espacio, pero todas son equivalentes.
Para completar damos las expresiones de las componentes no nulas del tensor de Ricci y del escalar de curvatura para el caso general de métrica FLRW:
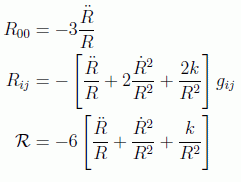
se puede ver aquí el detalle del cálculo con el software Mathematica.